Помогите.. Радиус окружности,описанной около правильного треугольника,равен 16 см.Вычислите отношение площади данного треугольника к площади круга,вписанного в данный треугольник....

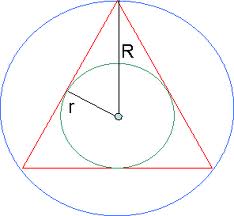
! Известны следующие правила(теоремы, св-ва...): радиус  окр-сти (круга) , описанной около прав. тр-ка   в 2 раза больше радиуса вписанной окр-сти (круга) ;

сторона прав. тр-ка равна произведению радиуса опис. окр. на √3.

1) SΔ/ S кр= (a²·√3/4):(πr²)

Найдём а и r.

a= R·√3= 16√3 (cм);  r =R/2= 16/2=8 (см), тогда

  SΔ/ S кр= (a²·√3/4):(πr²)=   ((16√3)²·√3/4):(π·8²)=( ¼·256·3√3)/ (64π)=3√3/π.

Ответ: в   3√3/π раз (приблизительно в 1,65 раз).