Предмет: Алгебра
Автор: Anniasua
Вопрос задан 1 год назад

< >

допоможіть будь ласка
sin x + sin 2x = 0

Аноним: скину розв‘язок в інст @mathematic_89

Anniasua: а почему

Anniasua: а чому не тут?

Ответы

Ответ дал: NNNLLL54

2

Ответ:

Решить уравнение . Применяем формулу синуса двойного угла .

$\bf sinx+sin2x=0\\\\sinx+2\, sinx\cdot cosx=0\\\\sinx\cdot (1+2\, cosx)=0\\\\a)\ \ sinx=0\ ,\ \ x=\pi n\ ,\ n\in Z\\\\b)\ \ cosx=-\dfrac{1}{2}\ \ ,\ \ x=\pm \dfrac{2\pi }{3}+2\pi k\ ,\ k\in Z\\\\Otvet:\ x_1=\pi n\ ,\ \ x_2=\pm \dfrac{2\pi }{3}+2\pi k\ \ ,\ \ n,k\in Z$

Приложения:

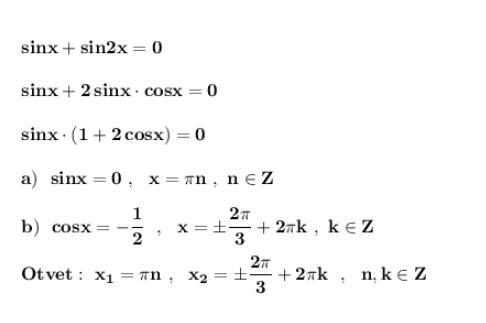
fctdgsygfdhngfxzgsac: NNNLLL54, здравствуйте! можете помочь пожалуйста?https://znanija.com/task/53925617

Похожие вопросы

Физика

1 год назад

8.Выберите из списка пару физических величин, которые всегда совпадают по направленню. А) сила и ускорение Б) сила и скорость В) ускорение и скорость 9. Согласно какому физическому закону тело

Алгебра

1 год назад

Помогите вирішать квадраті рівняння НУЖНО ОЧЕНЬ СРОЧНООООО, ПОЖАЛУСТА ПОМОГИТЕ!!!!!!!!!!!!!!!!!!!!!!!!!!!

Другие предметы

1 год назад

Довідавшись, що на світлі з вуглекислого газу й води утворюється глюкоза, шестикласник вирішив її отримати. Він поставив пляшку з газованою водою на яскравому світлі. Чи утворилася глюкоза? Чому?

Математика

1 год назад

как поделить столбиком 732 на 4

История

2 года назад

Який український вчений, зображений на грошовій куп заявляв про еднiсть людини і природи, Ул 1414141 tn 5004 cr, ||| 50 viru ge 1000 УКРАЇНА УКРАЇНА УКРАЇНА 500 п'ятсот ГРИВЕНЬ 50 П'ЯТДЕСЯТ гривень

Информатика

2 года назад

очень быстро запоминающее устройство небольшого объёма 1)оперативная память 2)кэш-память 3)постоянная память

Алгебра

8 лет назад

Помогите пожалуйста! Докажите, что выражение -y^2+2y-5 при любых значениях y принимает отрицательные значения.

Математика

8 лет назад

Условия задачи соединить с нужным вопросом чтобы получились задачи которые можно решитьусловие:1.За 30 мин. Наташа прошла 2 км 400м 2.Скорость Наташи 80м/мин 3.Расстояние