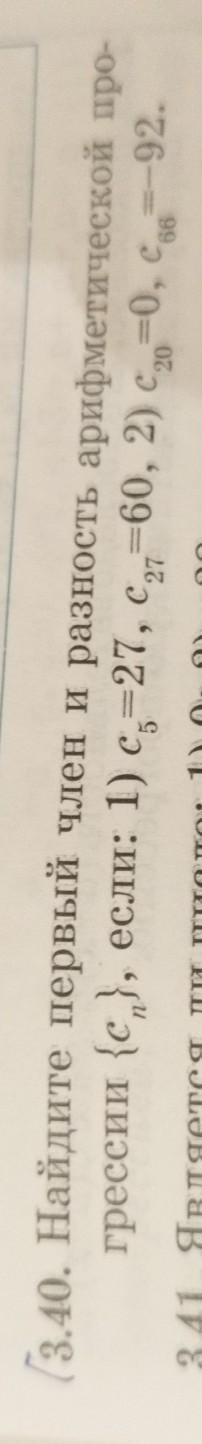помогите пожалуйста только 2​

Ответ: 1) 21 и 1,5

Объяснение:

1) Известна формула для нахождения значения любого члена арифметической прогрессии:

an = a₁ + d * (n - 1).

По условию задачи дано, что

а₅ =27, а₂₇ = 60

Подставим заданные значения в общую формулу:

 а) а₅ = а₁ + d * 4 = 27;

 б) а₂₇ = а₁ + d * 26 = 60

Получили систему из двух уравнений. Решать будем методом сложения:

26d - 4d = 60-27

22d = 33

d = 1.5 - разность арифметической прогрессии

подставим в одно из уравнений:

а₁ + d * 4 = 27

а₁ = 27 - 4d

а₁ = 27 - 4*1.5 = 21

а₁ = 21 - первый член арифметической прогрессии

2) аналогично:

Подставим заданные значения в общую формулу:

 а) а₂₀ = а₁ + d * 19 = 0;

 б) а₆₆ = а₁ + d * 65 = -92

19d + 65d = -92

84d = -92

 разность

а₁ + d * 19 = 0

 первый член