помогите пожалуйста. отдаю все баллы

Ответ:

Площа фігури обертання дорівнює 722π√3 см²

Объяснение:

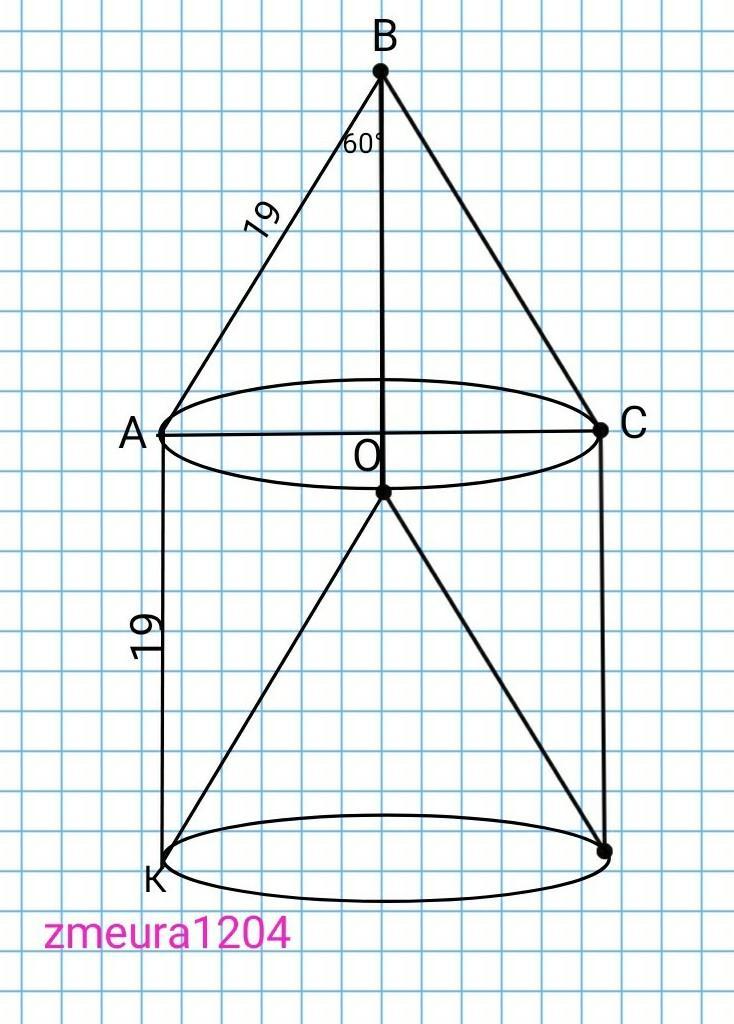
∠ABC=60°+60°=120°

∆ABC

Теорема косинусів:

АС=√(АВ²+ВС²-2*АВ*ВС*cos∠ABC)=

=√(19²+19²-2*19*19*cos120°)=

=√(361+361-2*361*(-½))=

=√1083=19√3 см діаметр.

R=AC/2=19√3/2=9,5√3 см.

Бічна поверхня складається з двох конусів і одного циліндра. R=9,5√3см радіус циліндра і конусів.

H=AK=AB=19см висота циліндра і образуюча конуса.

Конуси однакові.

Sб.к=πRH=π*9,5√3*19=180,5π√3см² бічна поверхня конуса.

Sб.ц.=2πRH=2π*9,5√3*19=361π√3 см² бічна поверхня циліндра.

Sфігури=2*Sб.к.+Sб.ц.=

=2*180,5π√3+361π√3=722π√3 см²