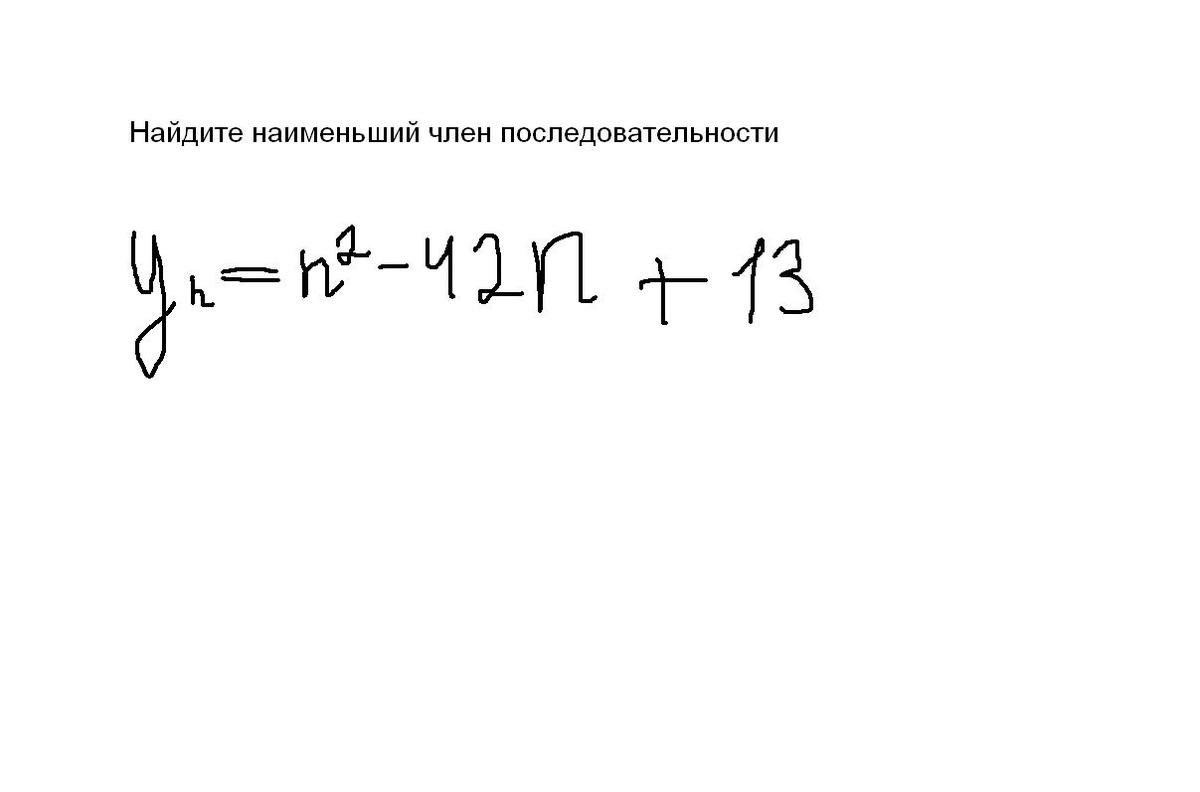Ответы
Ответ дал:
0
Так как последовательности задана квадратичной зависимостью, то используя свойства квадратичной функции

ветви параболы верх, значит наименьшее значение последовательности находится в вершине параболы, если n натуральное, иначе в одном из соседних натуральных чисел

вышло натуральное число - значит - это нужный номер члена последовательности (иначе смотрели бы по ближайшим натуральным)

ветви параболы верх, значит наименьшее значение последовательности находится в вершине параболы, если n натуральное, иначе в одном из соседних натуральных чисел
вышло натуральное число - значит - это нужный номер члена последовательности (иначе смотрели бы по ближайшим натуральным)
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад