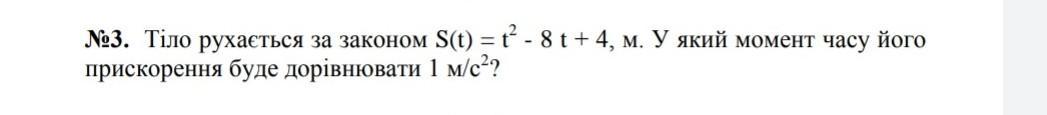Ответы
Ответ дал:
0
Прискорення \( a(t) \) визначається як похідна другого порядку від функції положення \( S(t) \) за відношенням \( a(t) = \frac{d^2S}{dt^2} \).
У даному випадку функція положення \( S(t) = 7t - 8t + 4 \), отже, шукана похідна другого порядку є нулем.
Отже, прискорення \( a(t) \) рівне нулю для будь-якого моменту часу \( t \) в даному випадку. Немає моменту часу, коли прискорення буде дорівнювати 1 м/с², враховуючи задану функцію положення.
У даному випадку функція положення \( S(t) = 7t - 8t + 4 \), отже, шукана похідна другого порядку є нулем.
Отже, прискорення \( a(t) \) рівне нулю для будь-якого моменту часу \( t \) в даному випадку. Немає моменту часу, коли прискорення буде дорівнювати 1 м/с², враховуючи задану функцію положення.
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад
8 лет назад