6. Стороны треугольника ABC равны: AB=3 см, BC=4 см, AC=5 см. Точка M равноудалена от каждой вершины на 5 см. Найти расстояние от точки M до плоскости L (альфа).
Обязательно напишите, что дано и сделайте чертёж.
Ответы
Ответ дал:
0
Дано: 


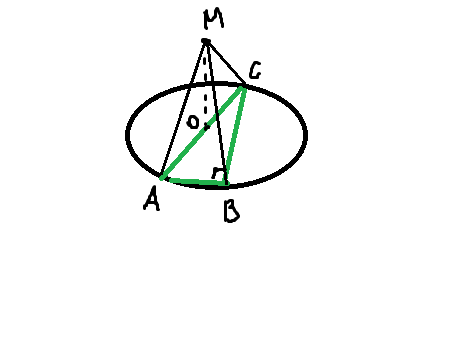
Решение: чтобы найти такую прямую, точки которой расположены одинаково далеко от вершин треугольника, нужно рассмотреть частный случай - найти такую точку в плоскости самого треугольника. Нетрудно догадаться, что эта точка - центр описанной окружности .
.
Рассмотрим . Это - египетский прямоугольный треугольник, что подтверждается теоремой Пифагора:
. Это - египетский прямоугольный треугольник, что подтверждается теоремой Пифагора:  . А центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы. Итак, радиус этой окружности равен
. А центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы. Итак, радиус этой окружности равен 
Рассмотрим прямоугольный треугольник . В нем
. В нем  . Третью сторону найдем по теореме Пифагора:
. Третью сторону найдем по теореме Пифагора:

Это и есть искомое расстояние от точки до плоскости
до плоскости 
Ответ:
Решение: чтобы найти такую прямую, точки которой расположены одинаково далеко от вершин треугольника, нужно рассмотреть частный случай - найти такую точку в плоскости самого треугольника. Нетрудно догадаться, что эта точка - центр описанной окружности
Рассмотрим
Рассмотрим прямоугольный треугольник
Это и есть искомое расстояние от точки
Ответ:
Приложения:
Ответ дал:
0
Все правильно. Ответ можно изобразить немного иначе, отчего он не изменится: МО=√(25-6,25)=√(25*25*3:100)=2,5√3 см
Похожие вопросы
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад