Шарик,брошенный под углом α=30 градусов к горизонту,оказался на высоте h спустя время t1=1 с и t2=2 с после начала полета.Определите модуль начальной скорости и высоту h.
Ответ: v0=30 m/c
h=10 m
Ответы
Ответ дал:
0
Совместим начало координат с точкой бросания и будем считать  Разобьем
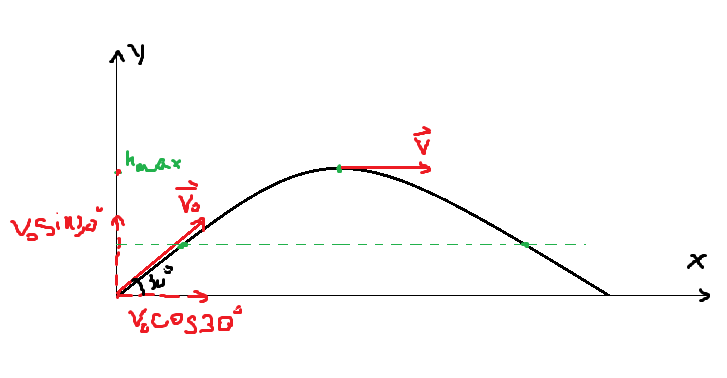
Разобьем  на составляющие:
на составляющие:

При движении под углом к горизонту, вертикальная составляющая скорости постоянно меняется, т.к. на тело действует сила тяжести, которая дает нашему шарику ускорение . Горизонтальная составляющая постоянна и равна
. Горизонтальная составляющая постоянна и равна  . Пока что запишем зависимость скорости в направлении оси
. Пока что запишем зависимость скорости в направлении оси  от времени.
от времени.

Далее смотрим на чертеж. Интуиция подсказывает, что между моментами и
и  точка достигает наивысшей высоты. Скорее всего эта точка находится посередине, т.е.
точка достигает наивысшей высоты. Скорее всего эта точка находится посередине, т.е.  . На самом деле так и есть! Движение подчиняется закону сохранения энергии, поэтому наша парабола симметрична.
. На самом деле так и есть! Движение подчиняется закону сохранения энергии, поэтому наша парабола симметрична.
Что же дальше? А дальше нам известно вот что: в момент вертикальная составляющая скорости равна нулю:
вертикальная составляющая скорости равна нулю:  (на рисунке если спроектировать вектор скорости в наивысшей точке на ось y, он окажется точкой, т.е. его длина по оси y равна нулю, а значит и скорость по оси y равна нулю). Обратимся к уравнению выше и подставим туда то, что мы только что поняли.
(на рисунке если спроектировать вектор скорости в наивысшей точке на ось y, он окажется точкой, т.е. его длина по оси y равна нулю, а значит и скорость по оси y равна нулю). Обратимся к уравнению выше и подставим туда то, что мы только что поняли.

Чтоб вычислить высоту нам нужно воспользоваться уравнением координаты.

Начальная координата равна нулю, начальная скорость по оси y равна половине начальной скорости, время t=t_max, а ускорение равно g, причем противоположно выбранному направлению (появится знак минус). Итак,

Немного отличается, зато у нас точнее.
При движении под углом к горизонту, вертикальная составляющая скорости постоянно меняется, т.к. на тело действует сила тяжести, которая дает нашему шарику ускорение
Далее смотрим на чертеж. Интуиция подсказывает, что между моментами
Что же дальше? А дальше нам известно вот что: в момент
Чтоб вычислить высоту нам нужно воспользоваться уравнением координаты.
Начальная координата равна нулю, начальная скорость по оси y равна половине начальной скорости, время t=t_max, а ускорение равно g, причем противоположно выбранному направлению (появится знак минус). Итак,
Немного отличается, зато у нас точнее.
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад