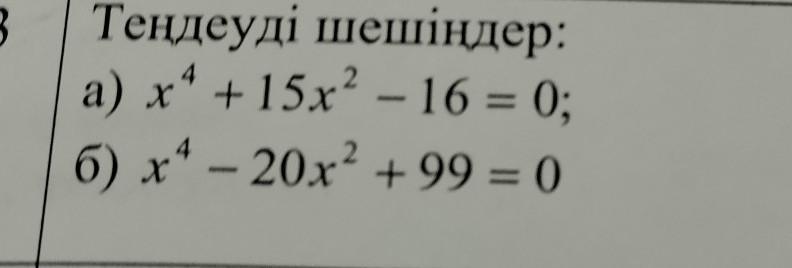Ответы
Ответ:
А)Дано квадратное уравнение:
\(x^2 + 15x^2 - 16 = 0\)
Для решения этого уравнения, сначала объединим подобные члены:
\(16x^2 - 16 = 0\)
Теперь приведем уравнение к стандартному виду квадратного уравнения \(ax^2 + bx + c = 0\):
\(16x^2 - 16 = 0\)
Разделим оба члена на 16:
\(x^2 - 1 = 0\)
Теперь у нас есть квадратное уравнение в стандартной форме. Мы можем решить его, применив факторизацию:
\((x - 1)(x + 1) = 0\)
Таким образом, у нас есть два возможных значения для \(x\):
1) \(x - 1 = 0\), откуда \(x = 1\)
2) \(x + 1 = 0\), откуда \(x = -1\)
Итак, решения квадратного уравнения \(x^2 + 15x^2 - 16 = 0\) равны \(x = 1\) и \(x = -1\).
Б)Дано квадратное уравнение:
\(x^2 - 20x^2 + 99 = 0\)
Для решения этого уравнения, сначала объединим подобные члены:
\(-19x^2 + 99 = 0\)
Теперь приведем уравнение к стандартному виду квадратного уравнения \(ax^2 + bx + c = 0\):
\(-19x^2 + 99 = 0\)
Так как коэффициент при \(x^2\) отрицательный, мы можем умножить оба члена на -1, чтобы получить положительный коэффициент:
\(19x^2 - 99 = 0\)
Теперь у нас есть квадратное уравнение в стандартной форме. Мы можем решить его, применив факторизацию или используя квадратное уравнение:
Факторизация:
\(19x^2 - 99 = 0\)
\((x - 3)(19x + 33) = 0\)
Таким образом, у нас есть два возможных значения для \(x\):
1) \(x - 3 = 0\), откуда \(x = 3\)
2) \(19x + 33 = 0\), откуда \(x = -\frac{33}{19}\)
Итак, решения квадратного уравнения \(x^2 - 20x^2 + 99 = 0\) равны \(x = 3\) и \(x = -\frac{33}{19}\).