Предмет: Алгебра
Автор: fctdgsygfdhngfxzgsac
Вопрос задан 1 год назад

< >

Знайти площу фігури, обмеженої кривою ........ прямими .... і ...... і віссю .....

Приложения:

Ответы

Ответ дал: pushpull

1

Ответ:

$\displaystyle S=\frac{46}{3}$

Объяснение:

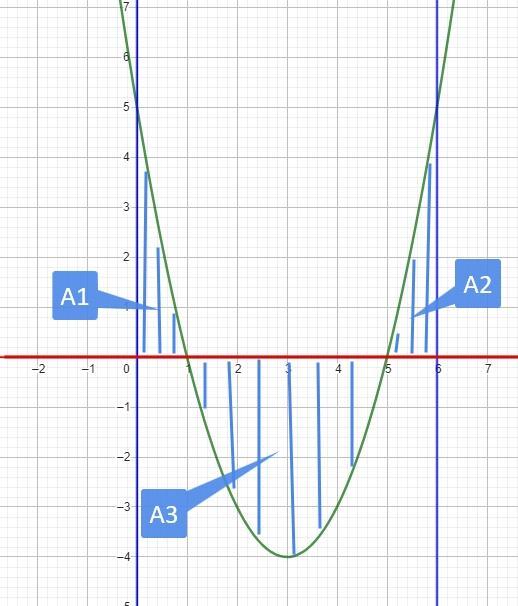
Как всегда, в первую очередь графики.

Из графиков понятно, что у нас две одинаковые фигуры А1 и А2 и еще одна фигура А3

Считаем площади фигур А1 и А2 путем нахождения площади одной фигуры и умножения результата на 2.

$\displaystyle S_{A1}=\int\limits^1_0 {(x^2-6x+5)} \, dx =\frac{x^3}{3} \bigg|_0^1-6*\frac{x^2}{2} \bigg|_0^1+5x \bigg|_0^1=\frac{1}{3} -3+5=\frac{7}{3}$

$\displaystyle S_{A1+A2}=2*\frac{7}{3} =\boldsymbol {\frac{14}{3} }$

Теперь посчитаем площадь А3

$\displaystyle S_{A3}=\int\limits^5_1 {(0-x^2+6x-5)} \, dx =-\frac{x^3}{3} \bigg|_1^5+6*\frac{x^2}{2} \bigg|_1^5-5x\bigg|_1^5=\frac{124}{3} +72-20=\boldsymbol{\frac{32}{3} }$

И тогда площадь искомой фигуры

$\displaystyle S=\frac{14}{3} +\frac{32}{3} =\frac{46}{3}$

Приложения:

fctdgsygfdhngfxzgsac: Спасибо большое)

Похожие вопросы

Английский язык

1 год назад

Уявіть, що ви власник школи англійської мови та наймаєте нового вчителя англійської мови. Запишіть три запитання, які ви б поставили людині, щоб перевірити, чи є вона кваліфікованим кандидатом на

Алгебра

1 год назад

ДОПОМОЖІТЬ БУДЬ ЛАСКА Алгебра 7 клас

Українська мова

1 год назад

13. Позначте рядок, у якому під час перенесення слiв допущено помилки: А) Прек - рас - ний, ход - жу, я - ма Б) Мо-ло-ко, со - няч-ний, вер - бо - ва В) Кар - ти-на, со-ло- вей-ко, ко- льоро- вий Г)

Українська література

1 год назад

лвоаоаоаоалаооааооаоашаоаолко

Английский язык

2 года назад

Записать одно отрицательное и одно вопросительное: 1. There is much snow in winter .2. There are 5 theatres in our city .3.There is no lift in our house .4.There are many new books in our library

Английский язык

2 года назад

помогите пожалуста очень срочно на завтра мне задали анг язык кто поможет того поблагодарю во задание составь и запиши вопросы по обратцу . you /f compter -Do you have a compter? 1)they ,funny toys

Математика

8 лет назад

Сравни. Поставь знак больше, меньше или равно. Пожалуйста!! заранее благодарю!!!

Литература

8 лет назад

отзыв по произведению Марка Твена Геккльбери Фина