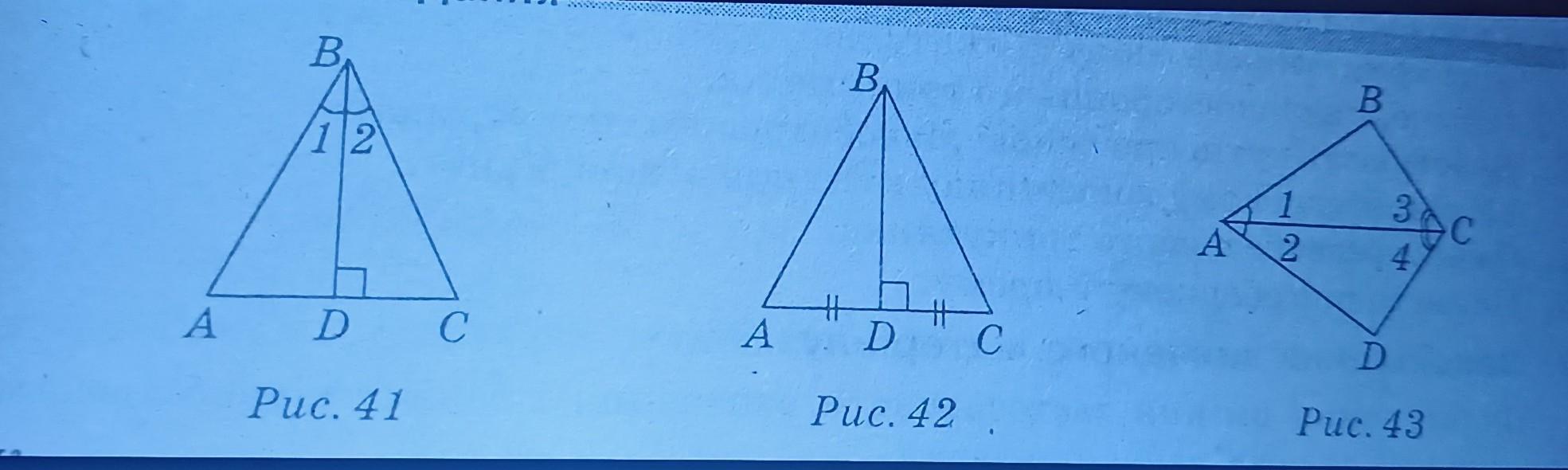
знайдіть трикутники, рівність яких можна довести і показати це доведення, рівні елементи позначені однаково
​

Відповідь:

1) ΔABD = ΔCBD, 2) ΔABD=ΔCBD, 3) ΔABC=ΔADC

Пояснення:

1) BD - висота трикутника ABC

∠ADB = ∠CDB = 90°

Отже ΔABD і ΔCBD - прямокутні

Розглянемо прямокутні трикутники ΔABD і ΔCBD

У них: BD - спільний катет, ∠ABD = ∠CBD (за умовою)

Отже, ΔABD = ΔCBD (за катетом і гострим кутом)

2) BD - висота трикутника ABC

∠ADB = ∠CDB = 90°

Отже ΔABD і ΔCBD - прямокутні

Розглянемо прямокутні трикутники ΔABD і ΔCBD

У них: BD - спільний катет, AD = CD (за умовою)

Отже, ΔABD=ΔCBD (за двома катетами)

3) Розглянемо ΔABC і ΔADC

У них: AC - спільна, ∠CAB = ∠CAD (за умовою), ∠ACB = ∠ACD (за умовою)

Отже,  ΔABC=ΔADC (за другою ознакою рівності трикутників)