Ответы
Ответ дал:
1
Ответ:
В данной задаче, у нас есть треугольник ОАВ, где ОА — касательная, ОВ — радиус круга, а ВС — отрезок касательной от точки касания до точки пересечения с другой касательной. Дано, что ОВ = 4 и ВС = 3.
С использованием свойства касательных, мы знаем, что касательная, проведенная к точке касания, перпендикулярна к радиусу, проведенному в эту точку. Поэтому треугольник ОВС — прямоугольный.
Мы можем использовать теорему Пифагора, чтобы найти длину ОС (гипотенузы):
ОС.2=ОВ.2+ВС.2
ОС.2=4.2+3.2
ОС.2 =16+9
ОС.2=25
ОС=5
Теперь, так как ОС — это радиус круга, и ОА — касательная, длина ОА будет равна длине ОС:
Длина ОА
=
5
Длина ОА=5
Пошаговое объяснение:
Приложения:
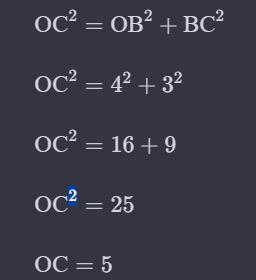
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад