Предмет: Геометрия
Автор: Jshshdhhdhdhdhbcncb
Вопрос задан 1 год назад

Дан прямоугольный треугольник. Найдите гипотенузу, если катеты треугольника относятся как 5 : 4, а высота, проведённая к гипотенузе, делит её на отрезки, один из которых на 18 больше другого.

Ответы

Ответ дал: natalyabryukhova

Ответ:

Гипотенуза равна 82 ед.

Объяснение:

Дан прямоугольный треугольник. Найдите гипотенузу, если катеты треугольника относятся как 5 : 4, а высота, проведённая к гипотенузе, делит её на отрезки, один из которых на 18 больше другого.

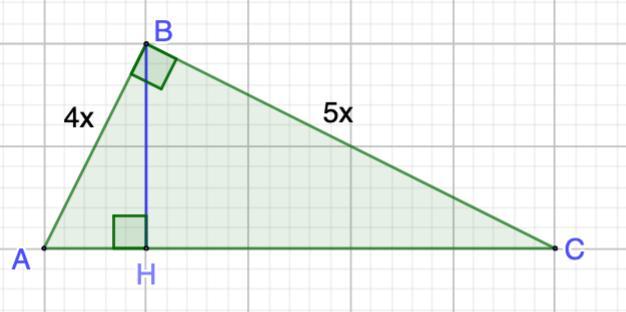
Дано: ΔАВС - прямоугольный (∠В = 90°);

ВН - высота;

ВС : АВ = 5 : 4; НС - АН = 18

Найти: АС

Решение:

ΔАВС - прямоугольный.

ВС : АВ = 5 : 4

Пусть АВ = 4х, тогда ВС = 5х.

Теорема Пифагора:
Квадрат гипотенузы равен сумме квадратов катетов.

⇒ АС² = АВ² + ВС² = 16х² + 25х² = 41х² ⇒ АС = х√41

Квадрат катета прямоугольного треугольника равен произведению гипотенузы и проекции этого катета на гипотенузу.

$\displaystyle AB^2=AH\cdot AC\;\;\;\Rightarrow \;\;\;AH=\frac{16x^2}{x\sqrt{41} }=\frac{16x}{\sqrt{41} } \\\\ BC^2=HC\cdot AC\;\;\;\Rightarrow \;\;\;HC=\frac{25x^2}{x\sqrt{41} }=\frac{25x}{\sqrt{41} }$