Пожалуйста, решите сколько сможете:
№1 Решите неравенство
(2x + 6)/x <0
№2 Решите неравенство
|2x + 1| > 7
№3 (1-ое вложение) Сколько целых чисел удовлетворяют системе неравенств
№4 (2-ое вложение) Найдите область определения выражения
№5 (3-ье вложение) При каких значениях параметра p система неравенств имеет два целочисленных решения
Обязатльно нужно решение номеров 1,2,3. 4/5 желательно.
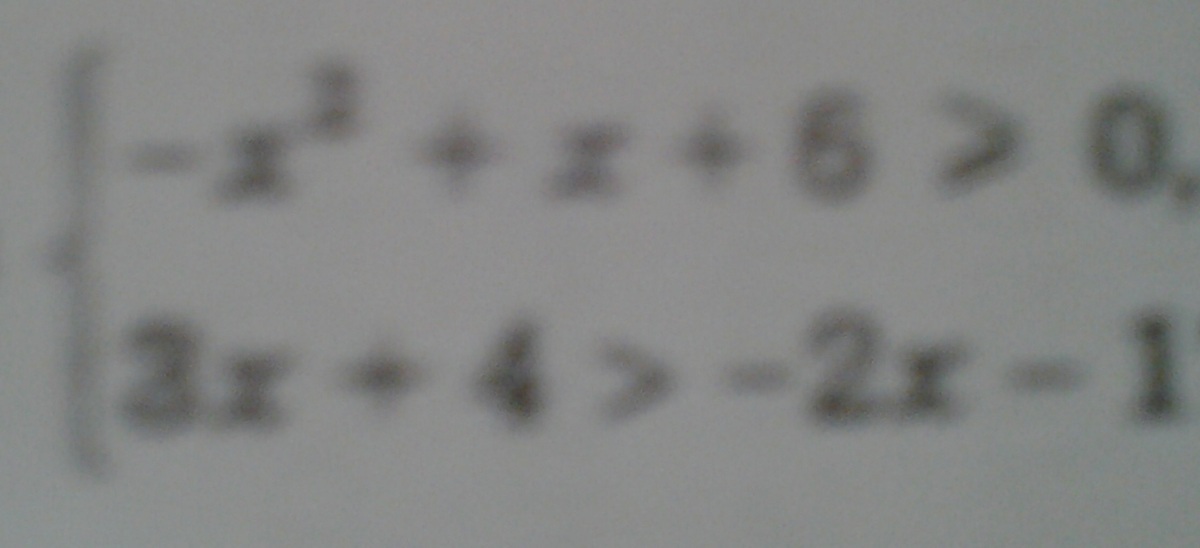
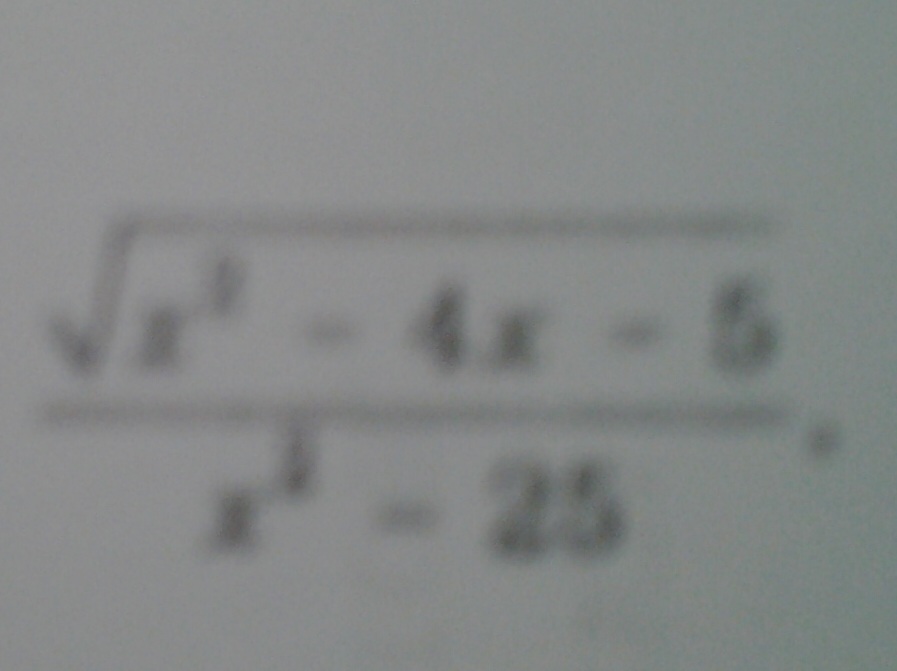
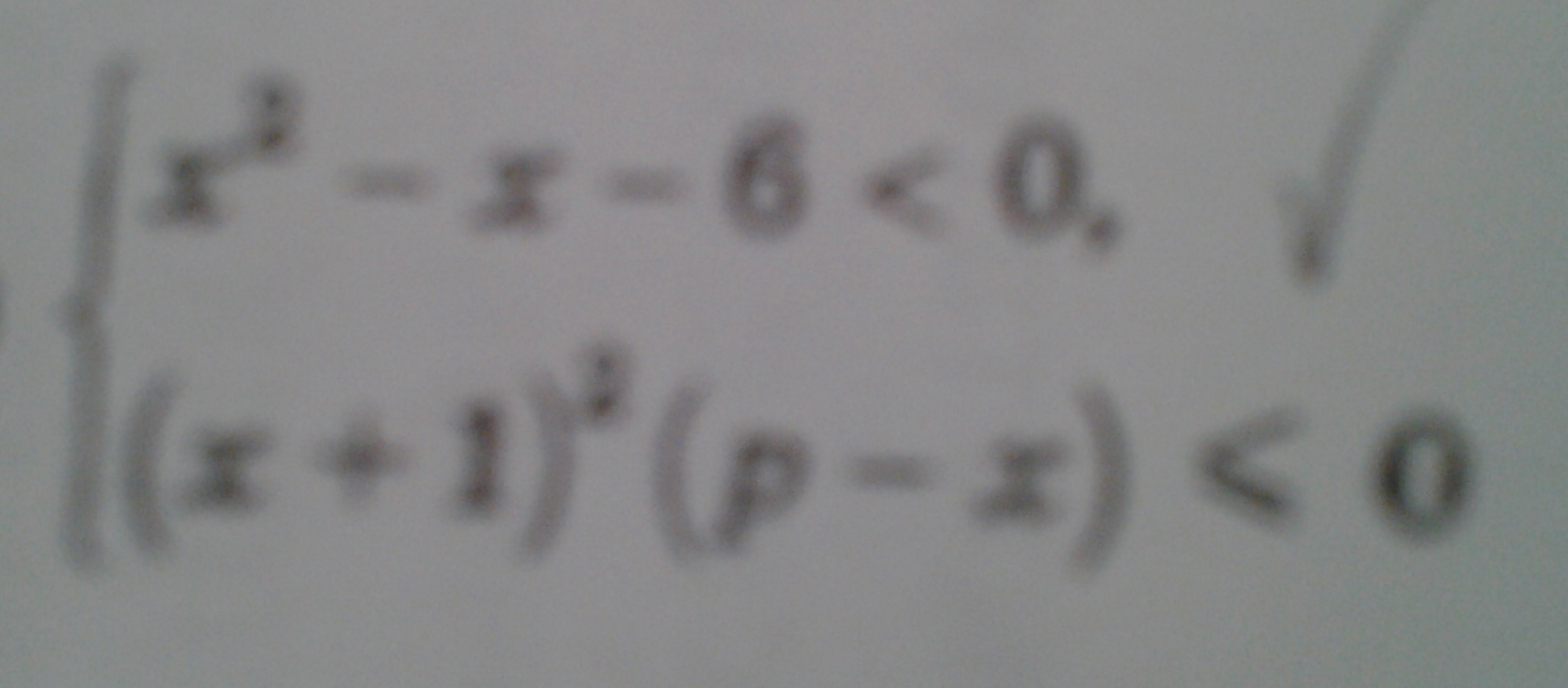
Ответы
1) числитель и знаминатель имеют разные знаки на отрезке ]-3;0[
2) 2x+1>7 2x>6 x>3
-2x-1>7 2x<-8 x<-4
ответ х>3 U x<4
3) решение первого неравенства ]-2;3[ решение второго x>-1 целочисленное решение системы 0; 1; 2 ответ число целочисленных решений 3.
4)x^2<>25 x<>5 U x<>-5
x^2-4x-5>=0 (x-5)(x+1)>=0 x<=-1 U x>=5
ООФ x>5 U x<-5 U -5<x<=-1
1) (2*x+6)/x<0
2x/x+6/x<0
2+6/x<0
6/x<-2
6< -2x
-6>2x
-3>x
x<-3
2)[2x+1]>7
[2x]>6
[x]>3
3)a.-x^{2}+x+6>0
x^{2}-x-6<0
D=1-4*1*(-6)=25 Корни вещественны
x1= (-(-1)+sqrt{-(-1)^{2}-4*1*(-6)})/2*1=(1+sqrt{25})/2=(1+5)/2=6/2=3
x2=(-(-1)-sqrt{-(-1)^{2}-4*1*(-6)})/2*1=(1-sqrt{25})/2=(1-5)/2=-4/2=-2
b. 3x+4>-2x-1
3x+2x>-1-4
5x>-5
x>-1
c. Из полученных решений x1=3, x2=-2, x>-1 получаем единственное целое число 3. Это ответ.