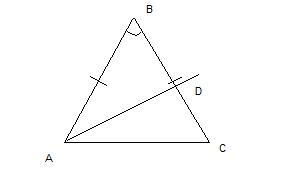
В треугольнике ABC  угол В равен 36градусов,AB=BC,AD-биссектриса.Докажите,что треугольник ACD-равнобедренный

 

1. Зная, что в равнобедренном треугольнике углы при основании равны, и сумма углов треугольника равна 180°, находим угол А и С:
<A = <C = (180 - 36) : 2 = 72°
2. Угол А делится биссектрисой пополам, значит, 
<DAC = 72 : 2 = 36°
3. Находим оставшийся неизвестный угол ADC в треугольнике ACD:
<ADC = 180 - 36 - 72 = 72°
Таким образом, <ADC = <C = 72°. Поскольку углы при основании DC в треугольнике ACD равны, значит он равнобедренный.