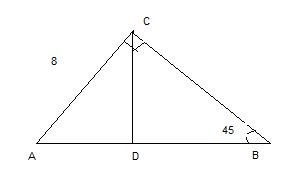
В прямоугольном треугольнике ABC<C=90 градусов,AC=8см, <ABC=45 градусов. Найти: а)AB; б)высоту CD, проведенную к гипотенузе.

1. Зная, что сумма углов треугольника равна 180°, находим угол А:
<A = 180 - 90 - 45 = 45°
Значит АВС - равнобедренный (углы при основании равны). АС = СВ = 8 см
2. Рассмотрим прямоугольный треугольник BDC:
sin B = CD : BC, отсюда CD = sin B * BC = sin 45 * 8 = √2/2 * 8 =  4√2 см
3. Зная катеты АС и СВ прямоугольного треугольника АВС, находим по теореме Пифагора АВ:
АВ = √AC² + CB² =√8² + 8² = √128 = 8√2 см