В правильной четырёхугольной призме ABCDA1B1C1D1 точки E и F- середины рёбер AD и DC соответственно.Найдите угол между прямыми B1D и EF.

АВСД, А1В1С1Д1 - квадраты (призма правильная)
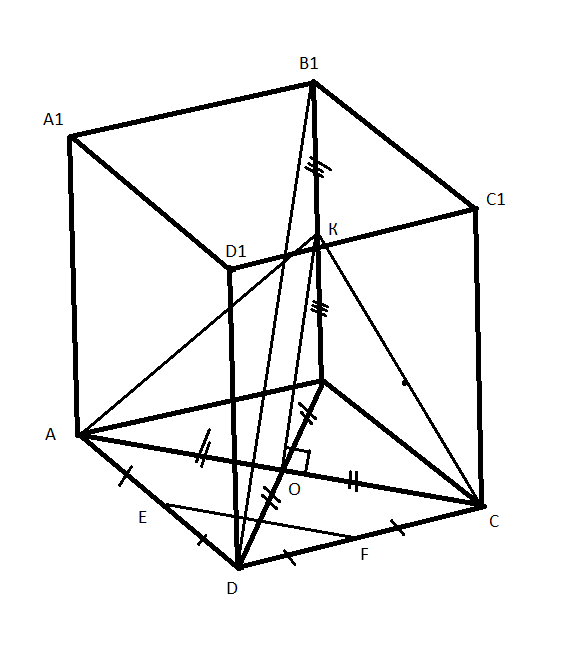
пускай О - пункт пересечения диагоналей АС и ВД квадрата АВСД,
раз точки E и F- середины рёбер AD и DC соответственно, то EF - средняя линия тр. АДС ⇒ АС ll EF
ВО = ОД (О - пункт пересечения диагоналей)
проведем в плоскости ВДВ1 прямую ОК, так, что ОК ll B1Д
тр. АКВ = тр. СКВ (по двум катетам) ⇒ АК = КС

дальше рассматриваем треугольник АКС, АО = ОС (О - пункт пересечения диагоналей) ⇒ КО - медиана
тр. АКС равнобедренный  ⇒ КО - высота ⇒ КО _l_ AC
а раз KO ll B1D  и  AC ll EF   ⇒ B1D _l_ EF

________________________________________________________________________

Спасибо большое! Вы мне очень помогли:)

нзч)