Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 150 градусов и 45 градусов. CD = 12 корней из двух.

Решите, пожалуйста.

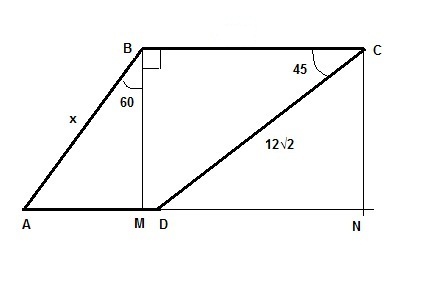
Вот рисунок.
AB = x, CD = 12√2; ABC = 150°, ABM = 150° - 90° = 60°; BCD = 45°
Треугольник CDN - прямоугольный  с углами 90°, 45° и 45°.
CN = BM = DN = CD/√2 = 12
Треугольник ABM - прямоугольный  с углами 90°, 60° и 30°.
x = AB = CN / cos ABM = 12 / cos 60 = 12 / (1/2) = 24