Задание С2 по математике

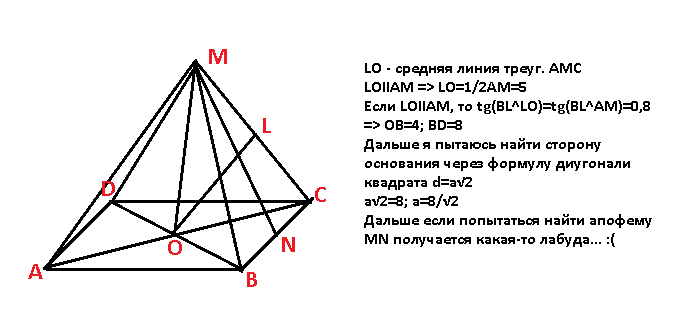
В правильной четырех угольной пирамиде MABCD с вершиной M боковое ребро равно 10. Точка L - середина ребра MC. Тангенс угла между прямыми BL и AM ранен 2√1/5. Найдите площадь боковой поверхности пирамиды.

ну тут находишь апофему MN= 2sqrt23;
далее рассмотрим треугольник MBC. его площадь равна
S= 1/2 * MN* BC= 4* sqrt46;
площадь боковой поверхности равна сумме площадей 4 граней, а т.к. они равны, следует, что S1=4*S=4*4*sqrt46=16*sqrt46

Все-таки решила сама:

Решение: LO=AM/2=5; tg(BL^AM)=tg(LO^LB)=2√1/5; OB=10V1/5; BD=20/√5; В треуг-ке BCD: cosB=45гр.=√2/2=BC/BD; BC=10√2/5; апофема MN= √90; Р=40√2/5; S=1/2*4*10√2/5*90=120