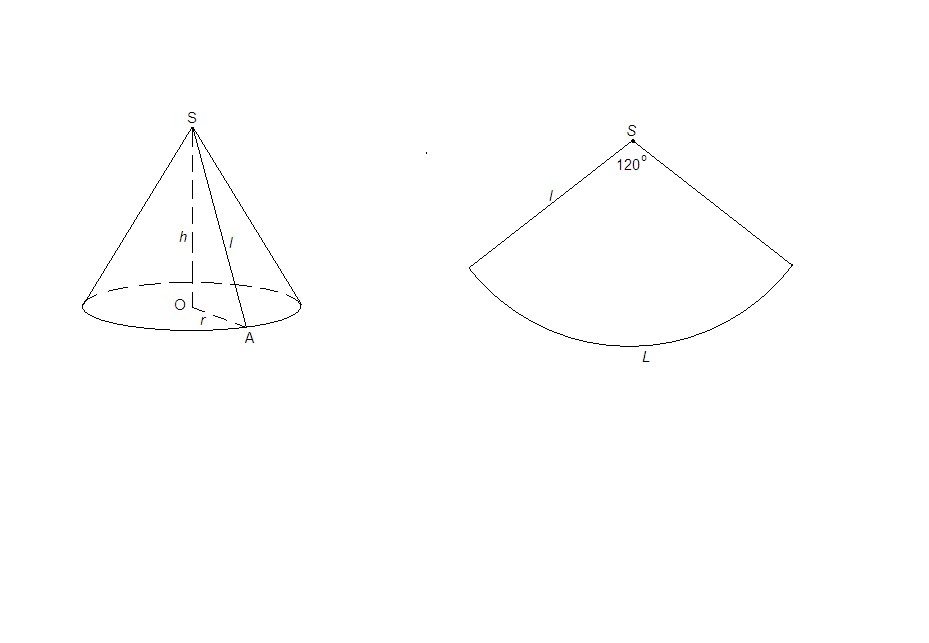
Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9см, а дуга равна 120 градусов
Ответы
Ответ дал:
0
В развертке боковой поверхности радиус R равен образующей конуса l, а длина дуги сектора L равна длине окружности основания С.
Длина дуги сектора:
L = (2πR · α)/360° = 2π · 9 · 120° / 360° = 6π см
Длина окружности основания:
С = 2πr
C = L, ⇒
2πr = 6π
r = 3 см
Sосн = πr² = 9π см²
ΔSOA: ∠O = 90°, по теореме Пифагора
h = √(l² - r²) = √(81 - 9) = √72 = 6√2 см
Длина дуги сектора:
L = (2πR · α)/360° = 2π · 9 · 120° / 360° = 6π см
Длина окружности основания:
С = 2πr
C = L, ⇒
2πr = 6π
r = 3 см
Sосн = πr² = 9π см²
ΔSOA: ∠O = 90°, по теореме Пифагора
h = √(l² - r²) = √(81 - 9) = √72 = 6√2 см
Приложения:
Похожие вопросы
2 года назад
10 лет назад
10 лет назад
10 лет назад