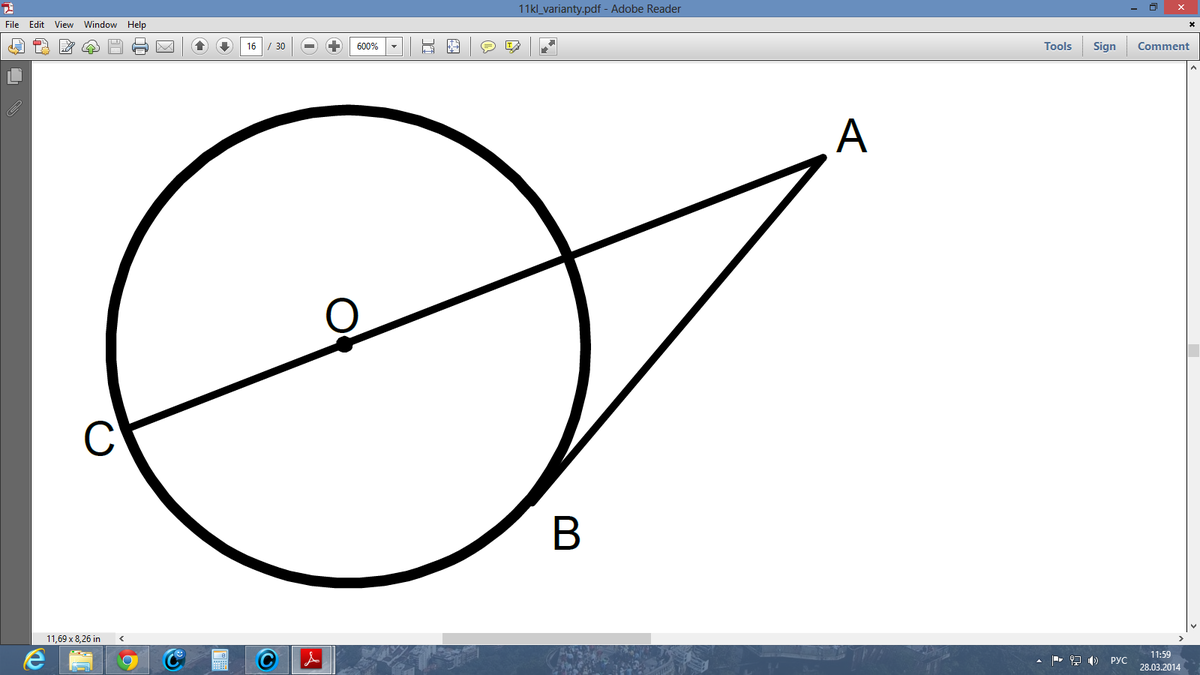
Одна сторона угла А,равного 35 градусов, касается окружности, а другая проходит через её центр.Найдите градусную величину меньшей дуги BC

В ответе должно получиться 125
Нужно решение

Соедините точку О с точкой В.
Так как АВ - касательная к окружности, то ОВ перпендикулярен к АВ. Рассмотрим прямоугольный треугольник ОАВ, угол А равен 35 град., угол ОВА равен 90 град.
Значит, угол АОВ равен:
<АОВ=180-(90+35)=55 град.
Рассмотрим отрезок СА. Он проходит через центр окружности и , значит, часть его, находящаяся внутри окружности, является ее диаметром. Угол СОА равен 280 град. Можно вычислить угол СОВ:
<СОВ-<АОВ=180-55=125 градусов. Это значит, что градусная мера дуги СВ равна 125 градусов.

Премного благодарен, только угол СОА наверное 180, а не 280

Конечно 180! Простите... Очень мелкий шрифт, а я плохо вижу. Лупы под рукой нет. Вы молодец, что заметили ошибку-описку! Успехов!