Ответы
Ответ дал:
0
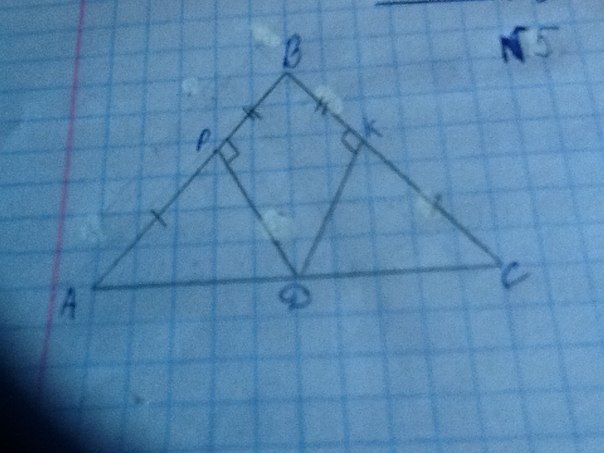
Дано: треугольник ABC, AP=KC, PB=KB, угол DPB = углу DKB = 90'.
Доказать: треугольник APD = треугольнику CKD.
Решение. Угол BPD = углу APD = 90', угол BKD = углу CKD =90'. Т.к. AP=KC, PB=KB, то AB=BC, следовательно, треугольник ABC-равнобедренный. Исходя из того, что треугольник ABC равнобедренный, получаем, что углы при основании равны, т.е. угол BAC = углу BCA.
Треугольник APD = треугольнику CKD по второму признаку равенства треугольников, т.к. AP=KC, угол BAC = углу BCA
и угол APD = углу CKD. Чтд.
Доказать: треугольник APD = треугольнику CKD.
Решение. Угол BPD = углу APD = 90', угол BKD = углу CKD =90'. Т.к. AP=KC, PB=KB, то AB=BC, следовательно, треугольник ABC-равнобедренный. Исходя из того, что треугольник ABC равнобедренный, получаем, что углы при основании равны, т.е. угол BAC = углу BCA.
Треугольник APD = треугольнику CKD по второму признаку равенства треугольников, т.к. AP=KC, угол BAC = углу BCA
и угол APD = углу CKD. Чтд.
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад