Из точки данной окружности проведены диаметр и хорда, равная радиусу. найдите угол между ними. пожалуйста сделайте ЧЕРТЕЖ,и решение!

Если сделать чертеж, то все сразу становится понятно.

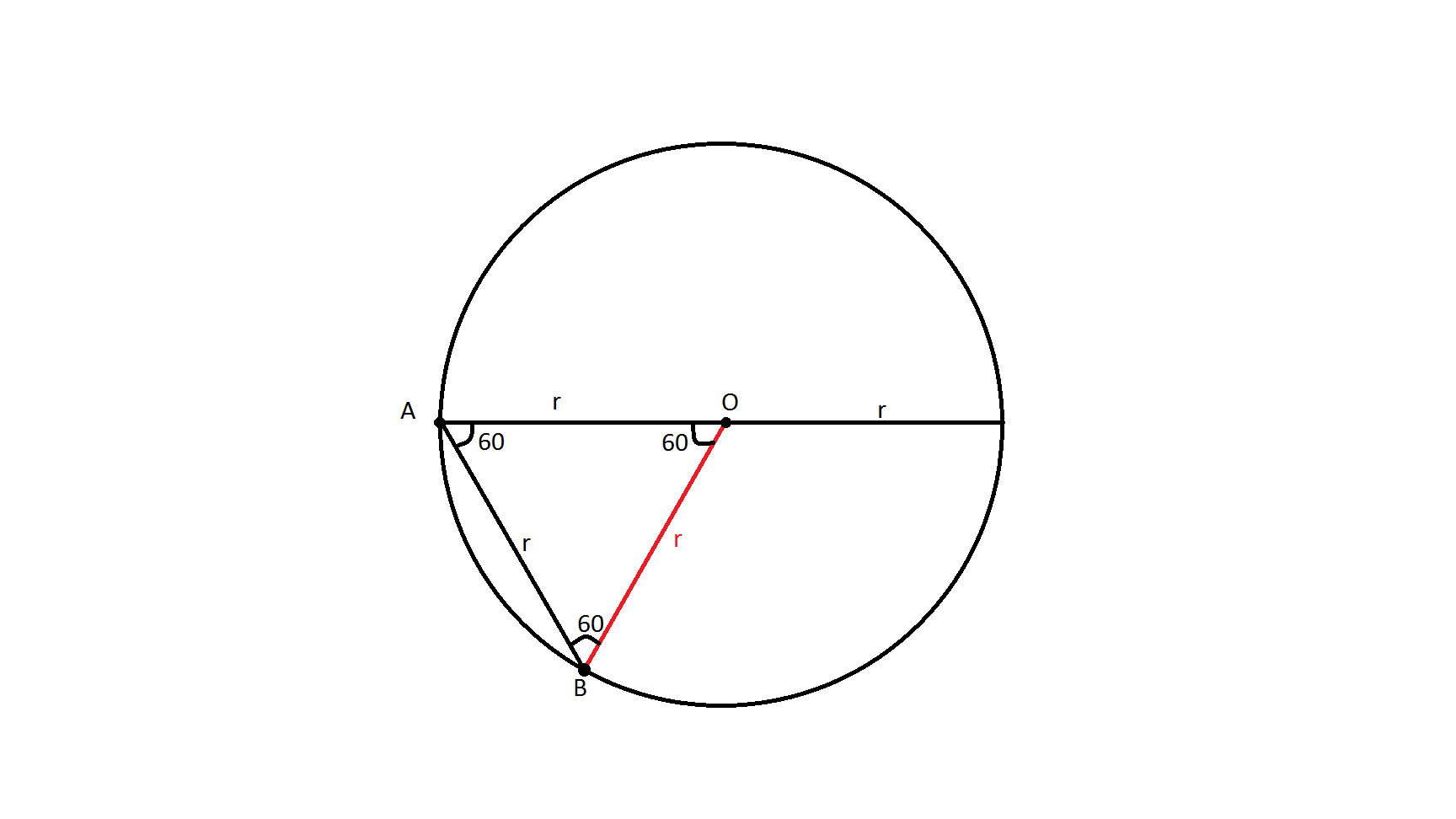
Обозначим центр окружности О. Исходную точку, из которой провели диаметр, проходящий через т.О, и хорду, равную радиусу, назовем точкой А. Точку пересечения окружности и хорды, назовем точкой В.

Достроим треугольник АВО, в котором АО и ВО - радиусы окружности, АВ - хорда, равная радиусу окружности, то есть:

АО=ОВ=АВ=r

Итого, мы получили равносторонний треугольник.

Как известно все углы в равностороннем треугольнике равны 60° (180/3=60)

Ответ: угол ОАВ=60⁰