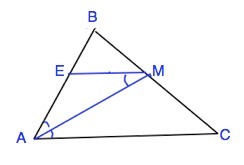
Отрезок АМ - биссектриса треугольника АВС. Через точку М проведена прямая, параллельная АС и пересекающая сторону АВ в точке Е. Доказать, что треугольник АМЕ равнобедренный.
Ответы
Ответ дал:
0
По условию ЕМ||АС, АМ - секущая. =>
угол ЕМА=углу МАС как накрестлежащие.
Биссектриса АМ делит угол ВАС пополам, и ∠ЕАМ=∠МАС.
Тогда ∠ЕМА=∠ЕАМ.
⇒ АМЕ равнобедренный по равенству углов при основании АС.
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад