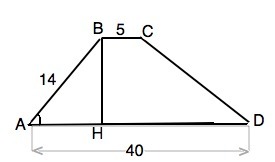
основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Ответы
Ответ дал:
0
Обозначим трапецию АВСD, ВН - высота, cos∠BAH=3/5.
cos ∠BAH=AH:AB=3/5 - это отношение катета и гипотенузы в "египетском" треугольнике, следовательно, второй катет ВН в ∆ АВН относится к гипотенузе как 4/5
ВН:АВ=sin∠ВАН=4/5
ВН=АВ• sin (ВАН)=14•4/5
Площадь трапеции равна половине произведения высоты на сумму оснований.
S(ABCD)=(BC+AD)•BH:2
S=45•28/5=252 (ед. площади)
----------------------
Высоту ВН можно найти и по т.Пифагора и через синус из основного тригонометрического тождества sin²α+cos²α=1.
Решение будет несколько длиннее, но приведет к тому же результату.
Приложения:
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад