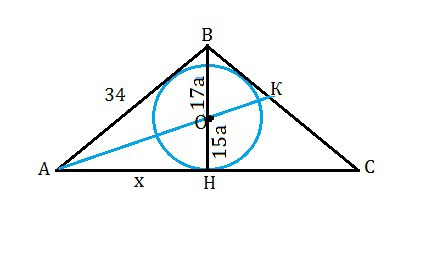
в равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17: 15, а боковая сторона равна 34 см. Найдите основание треугольника

Пусть этот треугольник АВС, АВ=ВС=34. 
ВН - высота, медиана. биссектриса этого треугольника и делит его пополам. ⇒
АН=СН
Центр вписанной окружности находится на пересечении биссектрис треугольника. 
Проведем биссектрису угла ВАС. 
Тогда она по свойству биссектрисы делит в треугольнике АВН  сторону ВН в отношении АВ:АН⇒
АВ:АН=17:15
34:АН=17:15⇒
АН=34•15:17=30 (см)
АС=АН+СН=60 (см)