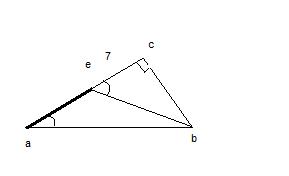
Дано треугольник abc . BE биссектриса  угол a равен 30 угол bec равен 60 .CE равно 7 см угол c равен 90 . Найти AE

В треугольнике bce находим угол ebc, зная, что сумма углов треугольника равна 180°:
<ebc=180-<c-<bec=180-90-60=30°
В прямоугольном треугольнике bce катет ес, лежащий против угла 30°, равен половине гипотенузы be. Отсюда
be=2*ec=2*7=14 см
Поскольку be - биссектриса, то <abe=<ebc=30°. Треугольник aeb - равнобедренный, т.к. углы при его основании ab равны. Значит ae=be=14 см