помогите с заданием! срочнооо!!!
Найдите наибольшее целое значение параметра m , при котором функция
f(x)=x^3/3 +m-3/2*x^2 +(m+5)*x - 17 возрастает на всей числовой прямой.
вот ф-ция..
Приложения:
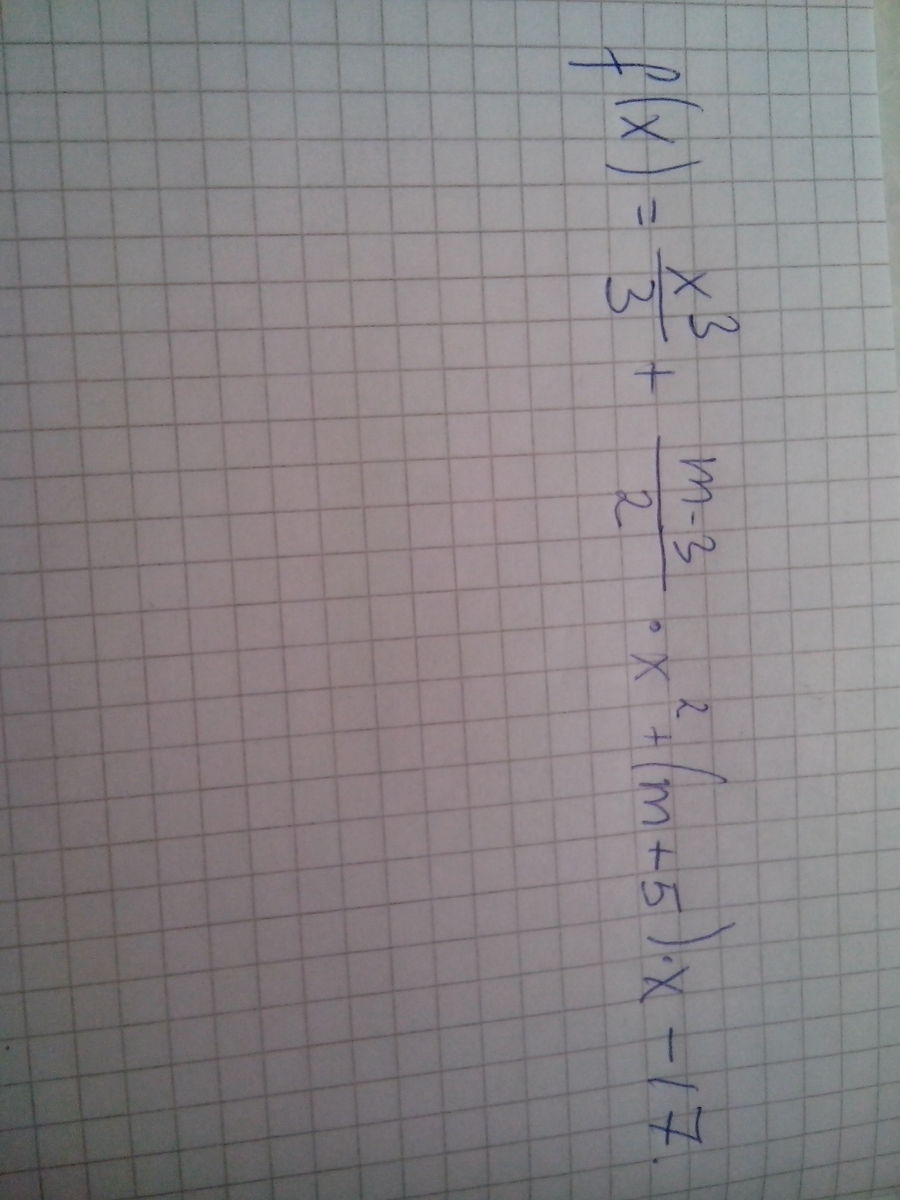
Ответы
Ответ дал:
0
f(x)=x^3/3+((m-3)/2)x^2 +(m+5)x-17
Функция возрастает на всей прямой, если ее производная неотрицательна
Берем производную
f'(x)=x^2+(m-3)x+m+5
Теперь решаем неравенство, удовлетворяющее нашему утверждению
x^2+(m-3)x+m+5>=0
D=(m-3)^2-4(m+5)=m^2-10m-11>=0
значит m C [-1;11]
Наибольшее значение m=11
Функция возрастает на всей прямой, если ее производная неотрицательна
Берем производную
f'(x)=x^2+(m-3)x+m+5
Теперь решаем неравенство, удовлетворяющее нашему утверждению
x^2+(m-3)x+m+5>=0
D=(m-3)^2-4(m+5)=m^2-10m-11>=0
значит m C [-1;11]
Наибольшее значение m=11
Похожие вопросы
7 лет назад
10 лет назад
10 лет назад
10 лет назад