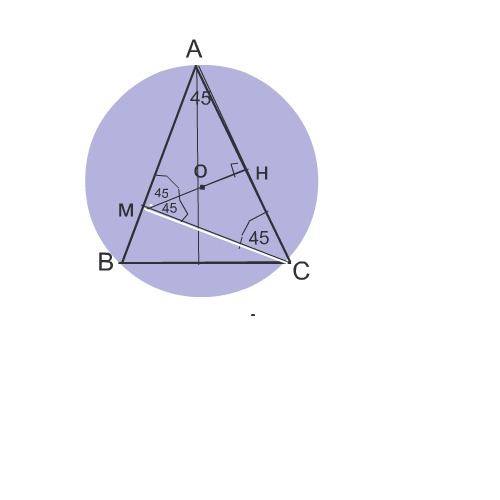
пожалуйста решите срочно. Равнобедренный треугольник ABC с основанием BC вписан в окружность с центром O. Площадь треугольника ABC равна 9 корень из 2, угол А =45 градусов. Прямая, проходящая через точку О и середину АС, пересекает сторону ВА в точке М. Найдите площадь треугольника ВМС

Площадь ᐃ  ВМС= площадь ᐃ  АВС минус площадь ᐃ  АМС
Обозначим точку пересечения прямой, проведенной из центра окружности, со стороной  АС - буквой Н.

Рассмотрим ⊿АМН
Он равнобедренный прямоугольный, так как прямая ОН, проведенная из центра окружности к хорде (а сторона АС - хорда) и делящая ее пополам, перпендикулярна ей, и отсюда угол АМН = 45°.

АН=НС по построению.

МН=НС и ⊿ МНС - равнобедренный прямоугольный .
Угол АМС=90°.
Итак, имеем равнобедренный прямоугольный ⊿ АМС
Обозначим АМ = МС = а.
АВ=АС, и, как гипотенуза равнобедренного прямоугольного треугольника, равна а√2.
СМ- высота ᐃ  АВС из вершины С к стороне АВ.
Запишем уравнение площади ᐃ  АВС
(а*а√2):2=9√2
а²√2=18√2
а²=18 см²
а=3√2 см
Теперь найдем площадь ⊿ АМС
S ⊿ АМС=АМ*МС:2=а²:2
S ⊿ АМС=(3√2)²:2=9см²
S ᐃ ВМС= 9√2-9=9(√2-1)см²