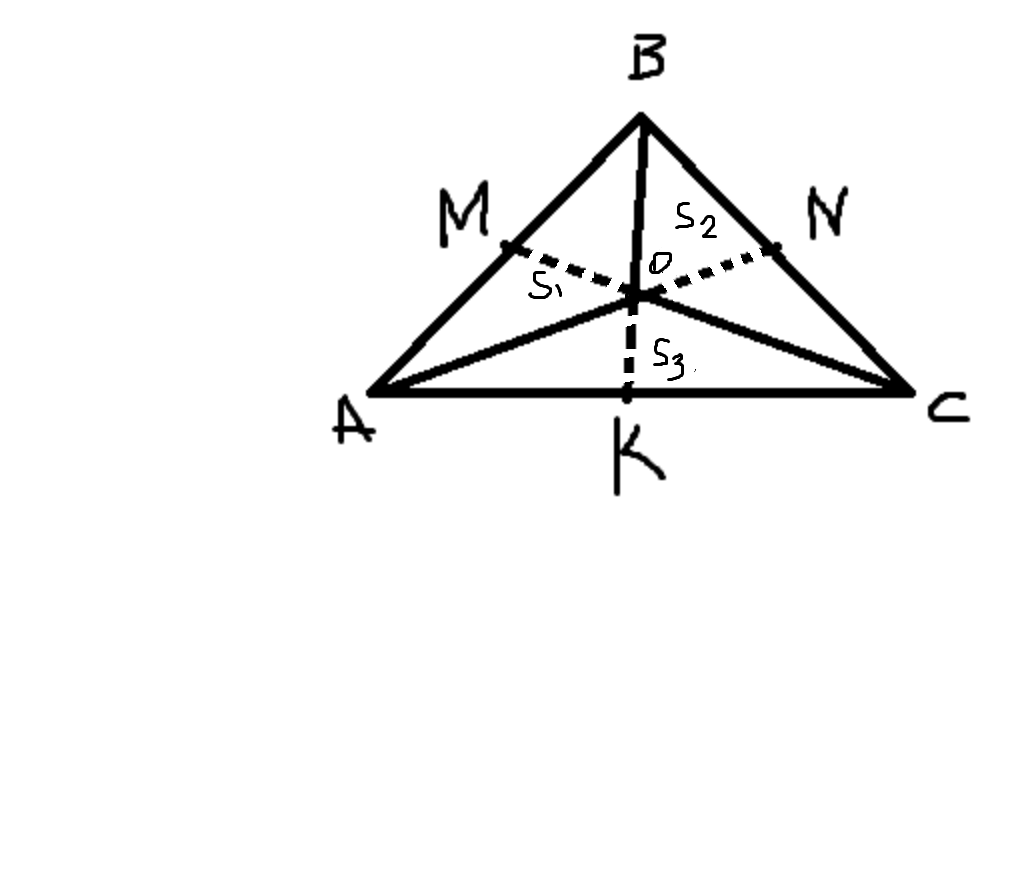
В треугольнике ABC медианы пересекаются в точке O. Докажите что площади треугольников AOB и CОА равны.
Ответы
Ответ дал:
0
Доказательство: Рассмотрим треуг.ABC. Проведем медианы из всех вершин, которые пересекаются в точке O. Получим треугольники треуг.AOB, треуг.BOC, треуг.AOC. Пусть их площади равны соответственно S1, S2, S3. А площадь треуг.ABC равна S. Рассмотрим треуг.ABK и треуг.CBK, они равной площади, т.к. BK медиана. В треугольнике треуг.AOC OK - медиана, значит площади треугольников AOK и COK равны. Отсюда следует, что S1 = S2. Аналогично можно доказать, что
S2 = S3 и S3 = S1 .
смотри файл вложен правда медианы не ровные
Приложения:
Похожие вопросы
2 года назад
2 года назад
10 лет назад
10 лет назад
10 лет назад