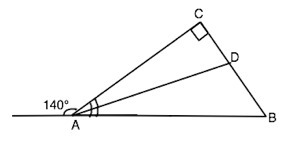
из вершины а прямоугольного треугольника авс с прямым углом с проведена биссектриса AD ,внешний угол при вершине равен 140.Найдите углы треугольника BDA
Ребята помогите пожалуйста решить,очень срочно,заранее спасибо большое!) 

Внешний угол прямоугольного треугольника при вершине А равен 140°. 
Значит, смежный с ним угол САВ=180°-140°=40°. 
АD - биссектриса и делит угол САВ пополам. 
Угол САD=20°
Сумма острых углов прямоугольного треугольника 90°
∆ СDA- прямоугольный, ⇒ 
∠СDA=90°-∠CВD=70°
Для Δ BAD угол СВD - внешний и равен сумме двух внутренних, не смежных с ним. ⇒
∠DBA=70°-∠DAB=70°-20°=50°
∠ADB=180°-CDA=110°
∠DAB=20°