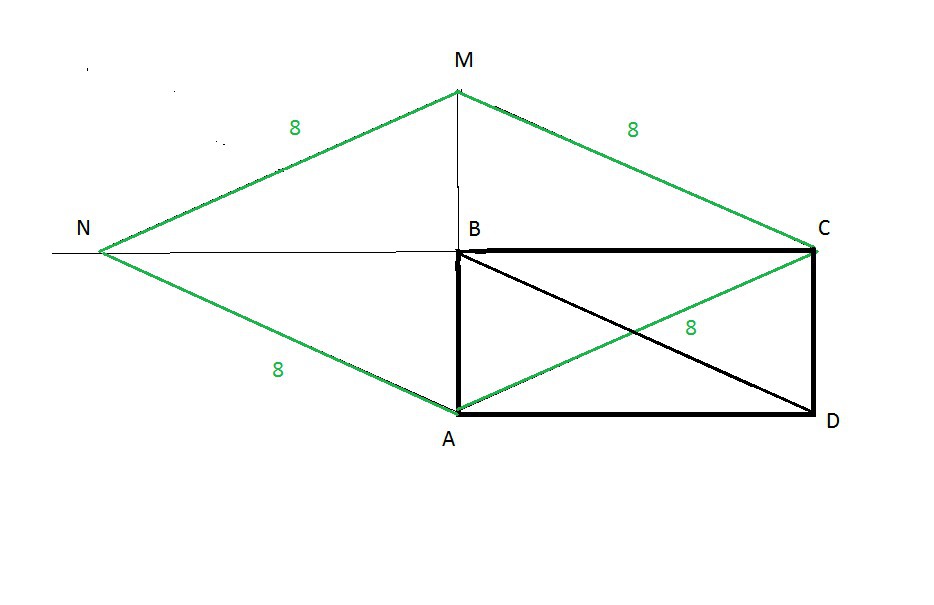
Через вершину C прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая пряму AB в точке M. Через точку M проведена прямая, параллельная диагонали AC и пересекающая прямую BC в точке N. Найдите периметр четырехугольника ACMN, если диагональ BD равна 8 см.

Диагонали прямоугольника равны
АС=BD=8 cм.

СМ ║ BD
BM ║ CD
BDCM - параллелограмм, значит MC=BD=8 cм

MN ║ AC
∠MNB = ∠BCA-внутренние накрест лежащие углы при параллельных прямых MN и АС и секущей NC.
АВ=СD=BM ⇒ AB=BM
ΔBMC =ΔABC  по катету и острому углу.
Из равенства треугольников следует равенство сторон
MN=AC=8 cм


ΔMNB = Δ ANB  по двум катетам.
NB- общий катет;
АВ=ВМ
Значит MN=NA=8 cм

Р( АCMN)=AC+CM+MN+NA=8+8+8+8=32 cм.

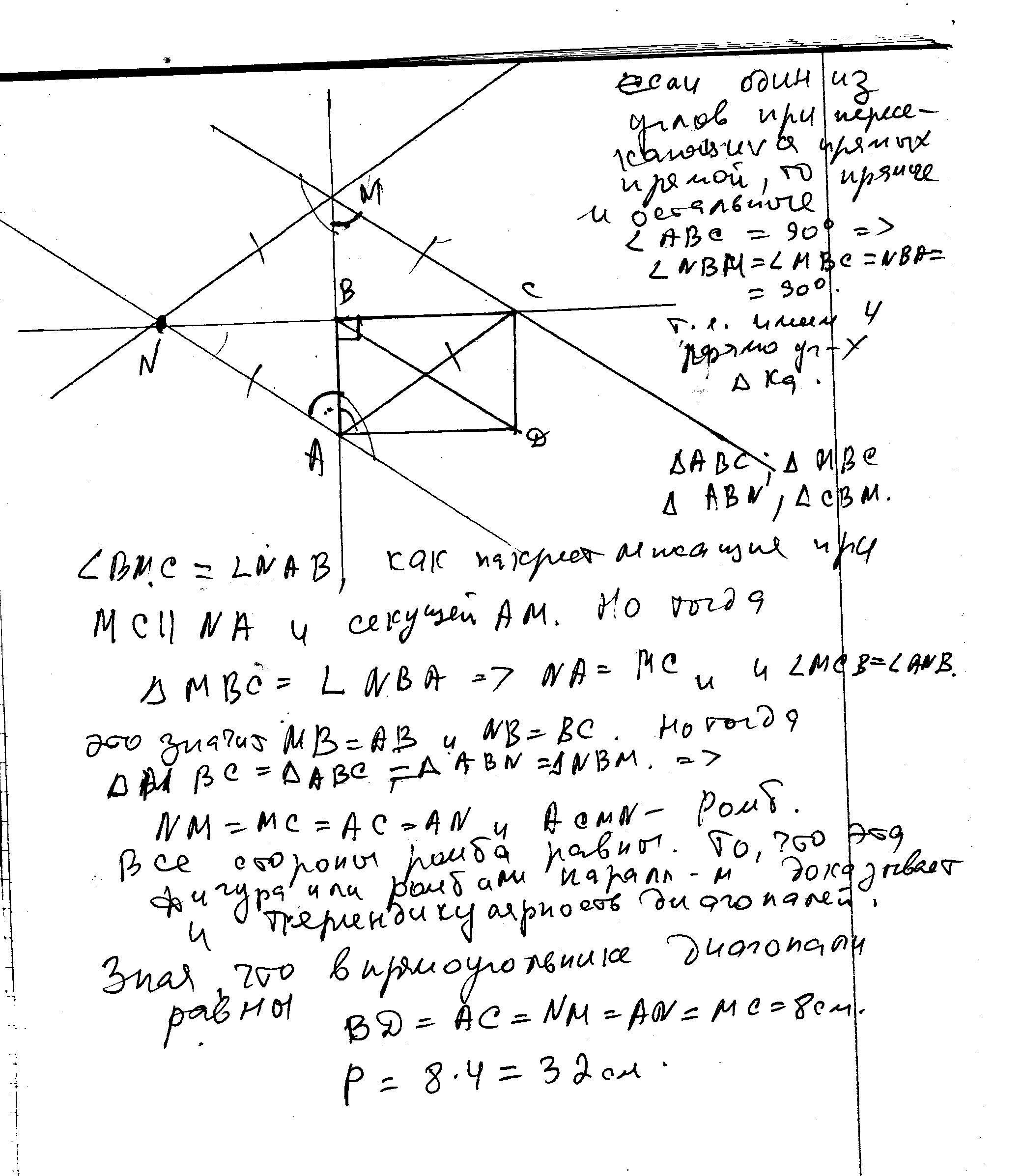
решение в скане..........