Угол amb равен 128 градусов, найдите угол mcb1 
Помогите пожалуйста очень надо!

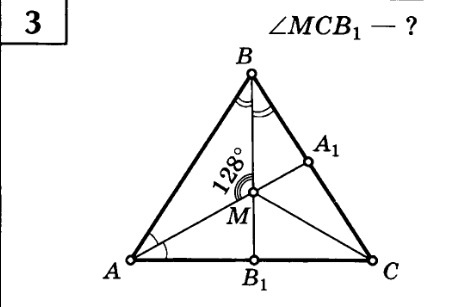
Биссектрисы треугольника пересекаются в одной точке. Поэтому можно сказать, что СМ - биссектриса также, и <MCB1=<MCA1=<C/2
Рассмотрим треугольник АМВ. Зная, что сумма углов треугольника равна 180°, запишем:
128+<BAM+<ABM=180, <BAM+<ABM=180-128
<BAM+<ABM=52°. Но по условию <BAM=<MАB1 и <ABM=<MBA1. Поэтому можно записать:
<MАB1+<MBA1=52°
В треугольнике АВС находим угол С:
<C=180-(<A+<B)=180-(<BAM+<MАB1+<ABM+<MBA1)=180-(<BAM+<ABM+<MАB1+<MBA1).
Чему равны суммы углов, мы записали выше. Значит наше выражение становится таким:
<C=180-(52+52)=76°
<MCB1=<C/2=76/2=38°