Найдите медиану, проведенную к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 8 см и 6 см.
Ответы
Ответ дал:
0
Сначала ищем гипотенузу АВ (она равна 10), значит половинки, которые на которые делит медиана гипотенузу равны 5. Рассмотрим получившиеся треугольники, прямой угол, который поделила медиана равен 45, острые углы В и А по определению равны 45 , а углы у основания мелианы равны 90. Значит эти треугольники равнобедренные, следовательно медиала равна половине гипотенузы, т. е. 5 см.
Ответ дал:
0
АВ=8СМ
АС=6СМ
АД-МЕДИАНА
АД=1/2 * КОРЕНЬ ИЗ(АВ^2+AC^2)=1/2 * КОРЕНЬ ИЗ(8^2+6^2)=1/2 *10=5 (СМ)
ОТВЕТ:5СМ
Приложения:
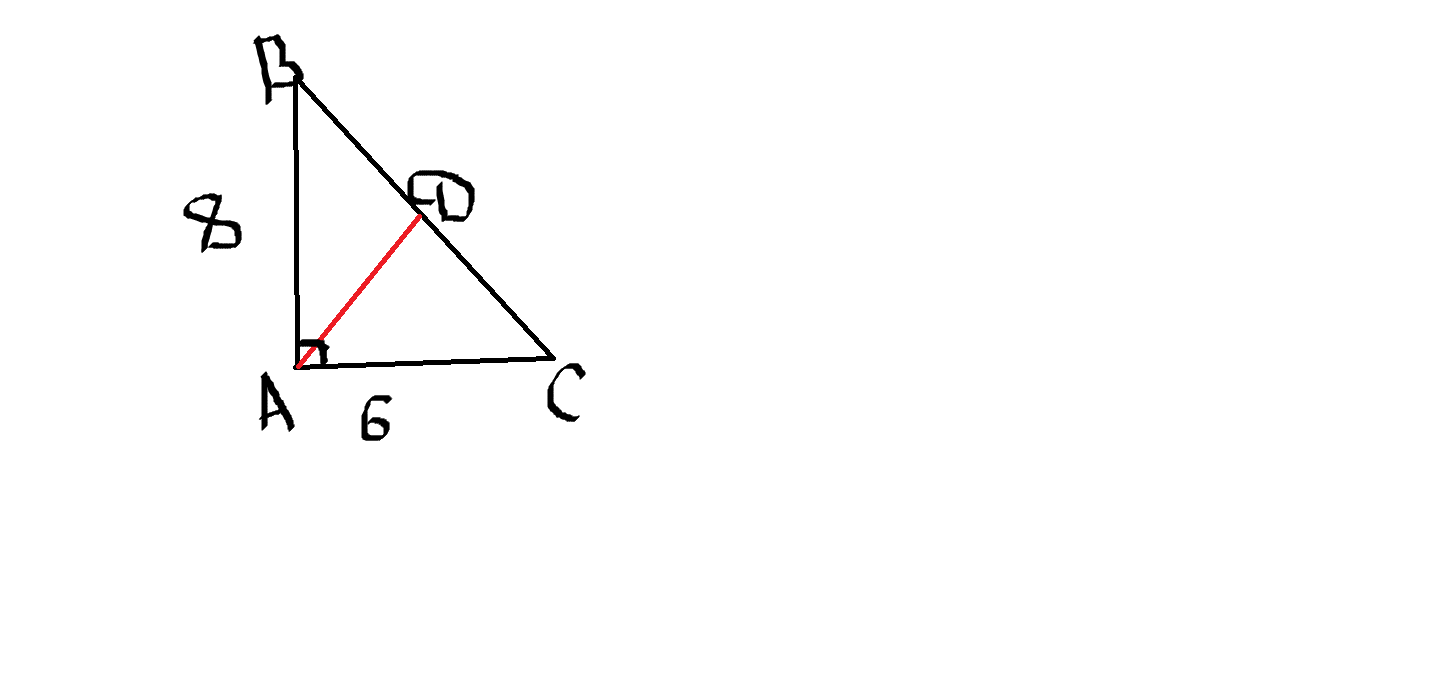
Похожие вопросы
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад