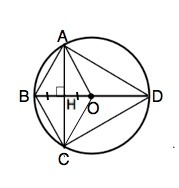
Отрезок BD-диаметр окружности с центром в точке О.Хорда АС делит пополам радиус ОВ и перпендикулярном к нему.Найдите углы четырёхугольника АВСD и градусные меры дуг АВ,BC,CD,AD.
Ответы
Соединим последовательно точки, лежащие на окружности, а точку А ещё с центром О.
∆ АОH - прямоугольный, АО - гипотенуза=R, ОН - 0,5R по условию.
соs∠AOH=0,5R/R=0,5. Это косинус 60°.
АО=ВО=R ⇒ в ∆АОВ углы при АВ равны 60°, и
∆ АОВ- равносторонний. Аналогично ∆ ВОС - равносторонний.
Дуга АВ=центральному углу АОВ=60°
Дуга ВС=дуге АВ=60°.
Центральные ∠АОD=∠COD=∠АОС=120° как суммы углов, равных 60°. Следовательно. дуга АD=дуге CD=120°
В четырехугольнике АВСD - ∠BAD=∠BCD=90° - опираются на диаметр.
∠АВС=2•60°=120°
∠АDС=половине центрального ∠АОС:2=120:2=60°
Дуги:АВ=BC=60°, CD=AD=120°