В правильной четырехугольной пирамиде сторона основания равна 6 см, а высота 4 см. Найдите площадь боковой поверхности пирамиды.

Sбок=12*Pосн*A,где A- апофема

Росн=6-4=24

А=КОРЕНЬИЗ 3^2+4^2=5

Sбок=12 * 24*5=60

Ответ: 60 см²

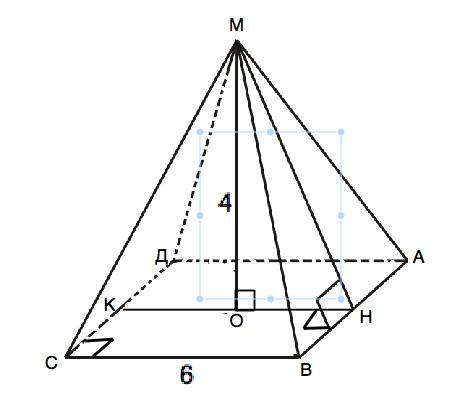
Объяснение: Пирамида правильная, ⇒ основание квадрат, боковые грани - равнобедренные треугольники, вершина пирамиды проецируется в центр основания.

  Пусть пирамида МАВСД, высота пирамиды МО.  Апофема МН⊥АВ, ⇒ по т. о 3-х перпендикулярах ОН⊥АВ и параллельно ВС.  ОН=КН:2==ВС:2, ОН=6:2=3.

Треугольник МОН - прямоугольный египетский, МН=5, ( то же самое по т.Пифагора МН=5).

Ѕ (бок)=МН•Р(АВСД)/2=5•4•6:2=60 см²