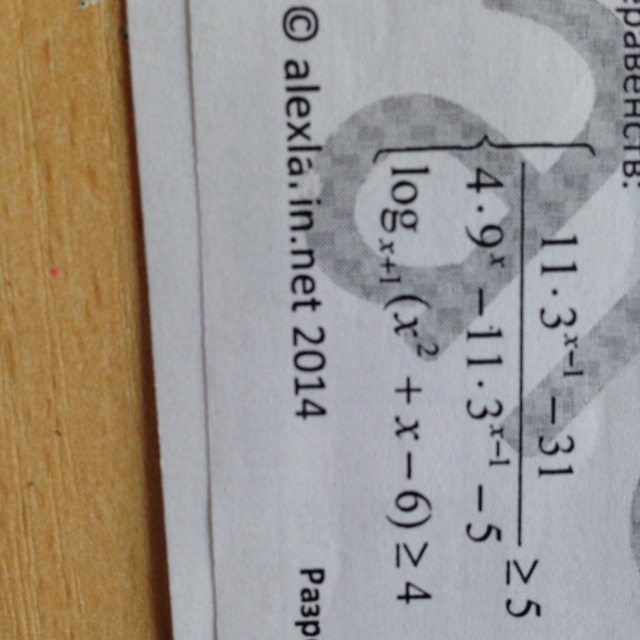Предмет: Алгебра
Автор: alexandrakk
Вопрос задан 10 лет назад

С3, пожалуйста, помогите решить второе неравенство!

Приложения:

Ответы

Ответ дал: Матов

$frac{11*3^{x-1}-31}{4*9^x-11*3^{x-1}-5} geq 5\\ log_{x+1}(x^2+x-6) geq 4\\$
$4*9^x-11*3^{x-1}-5=0\ 12*3^{2x}-11*3^x-15=0\ 3^x=t\ 12t^2-11t-15=0\ D=121+4*12*15=29^2\ t=frac{11+29}{24}=frac{5}{3}\ t=frac{11-29}{24}=-frac{3}{4}\ 3^x=frac{5}{3}\ x=log_{3}5-1=(0.5)\ (-infty;log_{3}5-1) cup (log_{3}5-1;infty)$
$1)\ frac{11*3^{x-1}-31}{4*9^x-11*3^{x-1}-5} geq 5\\ 11*3^{x-1}-31 geq 5(4*9^x-11*3^{x-1}-5)\\ 11*3^x-93 geq 15(4*9^x-11*3^{x-1}-5)\\ 11*3^x-93 geq 60*3^{2x}-5*11*3^x-75\\ 3^x=b\\ 11b-93 geq 60b^2-55b-75\\ 60b^2-66b+18 leq 0\\ 0.5 leq b leq 0.6\\ 3^x=frac{1}{2}\ x=log_{3}0.5\ 3^x=frac{3}{5}\ x=1-log_{3}5\ x in [log_{3}0.5;1-log_{3}5]\$
Решением первого неравенство будет $( - infty; -log_{3}2) cup [1-log_{3}5;log_{3}5-1)$
$2)log_{x+1}(x^2+x-6) geq 4\\ x^2+x-6>0\ (x+3)(x-2)>0\ (infty;-3) (2;+infty)\\ x^2+x-6 leq (x+1)^4\ x^2+x-6 geq x^4+4x^3+6x^2+4x+1\ x^4+4x^3+5x^2+3x+7 leq 0$
По графику видно что это неравенство не имеет решения .
Если перейти к графику $f(x)=x^4+4x^3+5x^2+3x$
она возрастает на всей числовой оси
То есть решений нет.

Ответ дал: МудрыйЕвреюшка

нет же. Видите подпись? Алекс Ларин, известный ЕГЭшник

Похожие вопросы

Русский язык

2 года назад

Можно ли назвать слова паук и паутина однокоренными?

Українська мова

2 года назад

Твір мініатюра "Найбільший мудрець-народ"

Литература

7 лет назад

Написать сочиние на произведение васюткино озеро по плану Кто такой васютка зачем мальчик отправился в тайгу почемузаблудился васютка что помогло васютке выжить втайге как повлияло на васютку