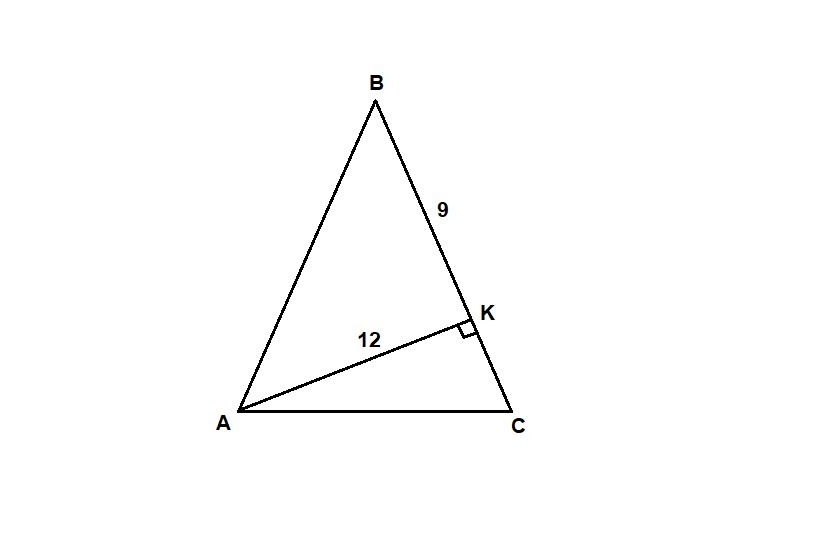
Высота АК остроугольного равнобедренного треугольника АВС (АВ = ВС) равна 12 см, а КВ = 9см. Найдите стороны треугольника АВС.

ΔAKB: ∠АКВ = 90°, по теореме Пифагора

           АВ = √(АК² + ВК²) = √(12² + 9²) = √(144 + 81) = √225

AB = 15 см

ВС = АВ = 15 см

KC = ВС - ВК = 15 - 9 = 6 см

ΔAKC: ∠АКС = 90°, по теореме Пифагора

           AC = √(АК² + КС²) = √(12² + 6²) = √(144 + 36) = √180

АС = 6√5 см