Предмет: Геометрия
Автор: freakishv
Вопрос задан 9 лет назад

четыре точки разбивают окружность на дуги, длины которых образуют геометрическую прогрессию со знаменателем 3. найдите меньший угол между диагоналями четырехугольника, полученного путем последовательного соединения этих точек.

Ответы

Ответ дал: Матов

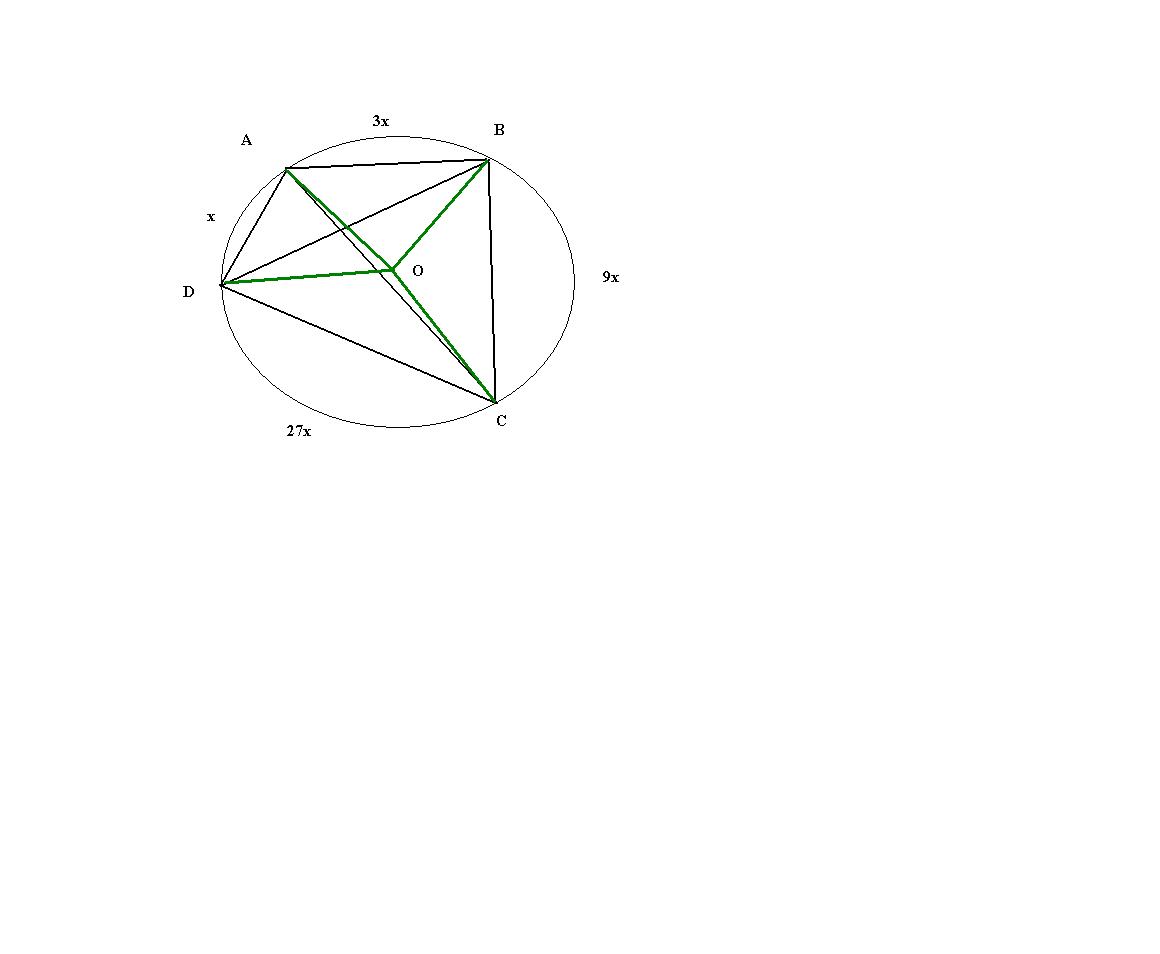
Ориентир по рисунку .
Полученный четырехугольник будет вписанным в окружность.
Так как дуги по формуле равны $L=frac{pi*r*n}{180}$ , где $n$ - центральный угол .
Пусть угол $AOD=n$ , дуга $wedge AD=x$ .
$x=frac{pi*r*n}{180}\ 3x=frac{pi*r*n_{1}}{180}\ 9x=frac{pi*r*n_{2}}{180}\ 27x=frac{pi*r*n_{3}}{180}\\ n+n_{1}+n_{2}+n_{3}=360\\ n_{1}=3n\ n_{2}=9n\ n_{3}=27n \ n=9а\ n_{1}=27а\ n_{2}=81а\ n_{3}=243а$ ,
Заметим что углы $BDC BOC$ итд опираются на одну и ту же дугу.
По теореме о вписанном угле , вписанный угол $BDC=frac{BOC}{2}$
выражая все углы
получим
$BDC=40.5а\ ADB=13.5а\ CBD=121.5а\ ABD=4.5а\$
$ACB=13.5\$
тогда угол между диагоналями
$180-121.5-13.5=45$ он самый наименьший

Приложения: