В трапеции ABCD боковая сторона CD равна 12, а расстояние от середины стороны AB до прямой CD равно 5. Найдите площадь трапеции.

См. Чертеж.

Треугольники ЕВС и МАЕ равны (ЕА = ЕВ, и углы ЕВС и ЕАМ, и МЕА и ВЕС - попарно равны). Поэтому МА = ВС. Расстояние от Е до АD равно половине высоты трапеции, а МD равно сумме оснований. Поэтому площадь треугольника MDE равна половине площади трапеции. но площадь МDE равна сумме площадей ВЕС и АЕD. Получается, что площадь треугольника CED равна половине площади трапеции ABCD. 

Площадь CED равна (1/2)*ЕК*СD, поэтому площадь трапеции

S = EK*CD = 5*12 = 60

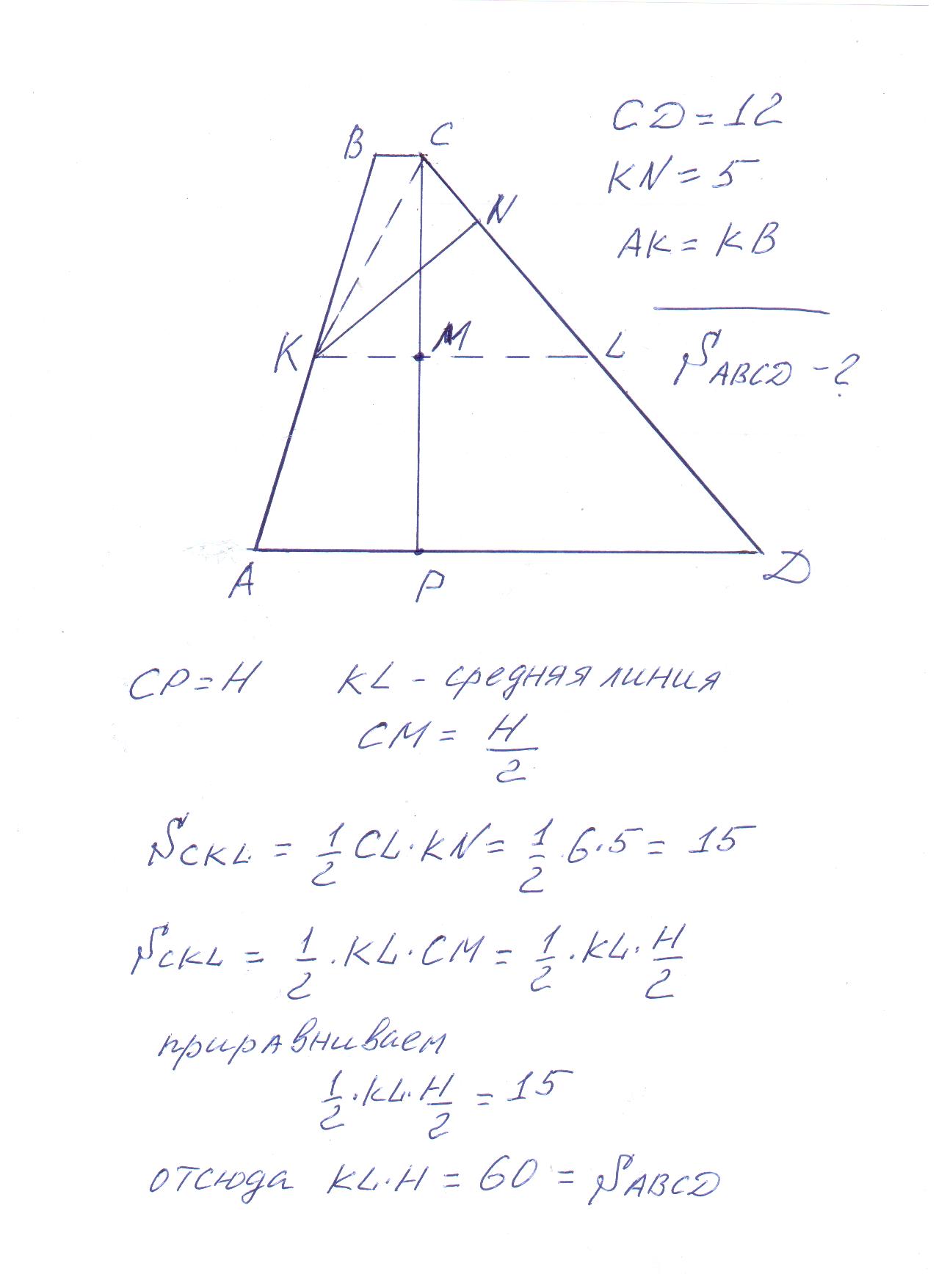
Через точку К проведём прямую КL параллельно АД. То есть КL-это средняя линия трапеции АВСД, далее смотри рисунок.