Два шарика массой 1 г каждый подвешены на нитях,верхние концы которых соединены вместе.Длина каждой нити 10 см.Какие одинаковые по величине заряды можно сообщить шарикам,чтобы нити разошлись на угол 60 градусов?

Дано:

Масса шариков: m = 1 г = 0,001 кг.

Длина нити: L = 10 см = 0,1 м.

Угол между нитями: β = 60°.

Найти нужно заряды на шариках: q - ?

Решение:

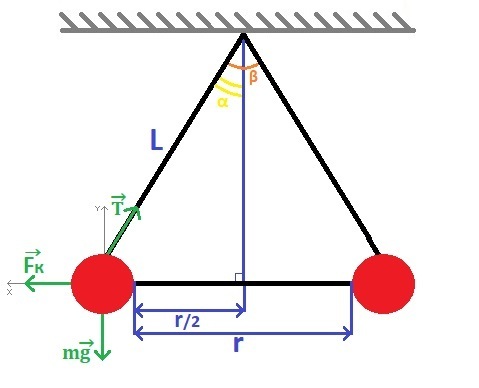
1. Построим рисунок (см. приложение). Рассматривая силы действующие на шарик, будем иметь дело с углом

2. Запишем второй закон Ньютона для одного шарика:

3. Возьмём проекцию на ось Оy:

4. Выразим из (3) силу натяжения нити:

5. Возьмём проекцию на ось Оx:

6. Объединяем (4) и (5):

7. Вспоминаем формулу силы кулоновского взаимодействия:  , учитывая, что заряды одинаковы:

8. Из геометрии имеем:

9. Объединяем (6), (7) и (8):

10. Выразим заряд из (9), вспомним угол β:

Прошу не удивляться знаку "±" перед корнем. Отталкиваться будут как два положительных, так и два отрицательных заряда. Более того, алгебраически, извлекая корень чётной степени, необходимо учитывать оба знака.

Численно получим:

(Кл).

Переведём в нанокулоны:   Кл = ± 80 нКл.

Ответ: 80 нКл, или -80 нКл.