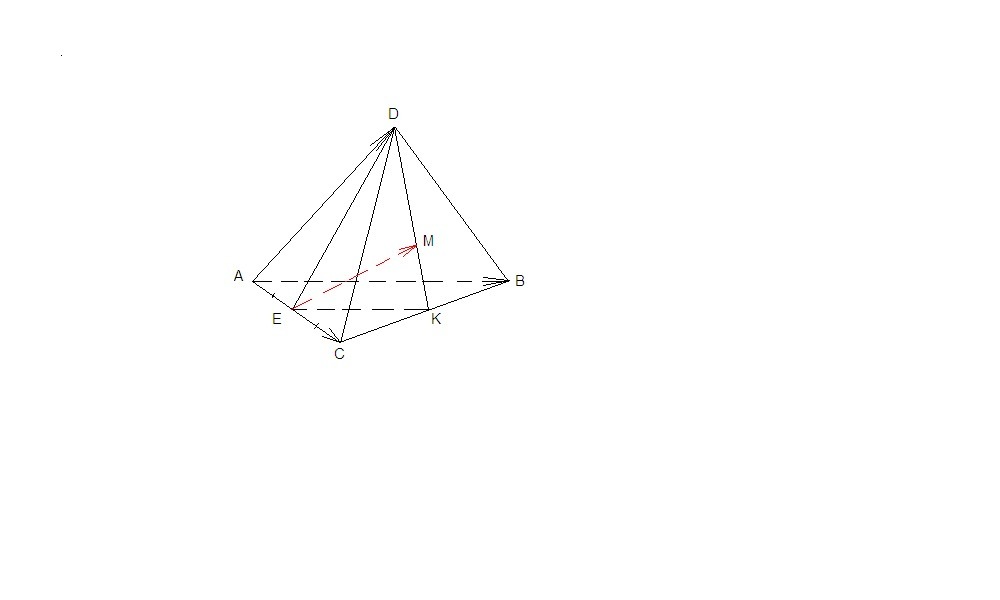
В тетраэдре DABC M-точка пересечения медиан грани BDC, E-середина AC. Разложите вектор EM по векторам AC , AB и AD

Если DK - медиана грани DCB, то ЕК - средняя линия ΔАВС.
↑KD = ↑KE + ↑ED
Так как точка пересечения медиан М делит медианы в отношении 2 : 1, считая от вершины, то
↑KM = 1/3↑KD = 1/3(↑KE + ↑ED)
↑EM = ↑EK + ↑KM = ↑EK + 1/3↑KE + 1/3↑ED = ↑EK - 1/3↑EK + 1/3↑ED =
= 2/3↑EK + 1/3↑ED

↑EK = 1/2↑AB так как средняя линия параллельна основанию и равна его половине.
↑ED = ↑EA + ↑AD = - ↑AE + ↑AD = - 1/2↑AC + ↑AD

↑EM = 2/3 · 1/2↑AB + 1/3(- 1/2↑AC + ↑AD)
↑EM = 1/3↑AB - 1/6↑AC + 1/3↑AD