напишите уравнение прямой, проходящей через начало координат, которая параллельна касательной к графику функции y(x)= , проведенной в точке M(-1;y(-1))
Ответы
Ответ дал:
0
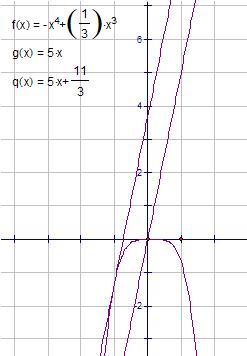
Уравнение прямой Y=kx+b. Так прямая проходит через начало координат, то 0=k*0+b,
b=0. Найдем к. y '(x) = -4x^3 + x^2. к = y '(-1) = 4+1=5 (значение производной в абсциссе точки касания равно угловому коэффициенту касательной к)
Уравнение прямой Y=5x
Иллюстрация во вложении
Приложения:
Похожие вопросы
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад