SACD- правильная четырехугольная пирамида, все ребра которой равны между собой. Точки О и К - середины ребер SD и SC соответственно. Точка F лежит на продолжении ребра AD так, что точка D есть середина отрезка AF. Постройте точку, в которой прямая L, проходящая через точку F и параллельной прямой AB, с плоскостью SBC. Вычислите площадь боковой грани пирамиды, если площадь четырехугольника FOKT равна 9корень из 3 см кв.
Ответы
Ответ дал:
0
применено: теорема Пифагора, формулы площади трапеции и треугольника, формула высоты правильного треугольника, свойство средней линии треугольника; свойство параллельных прямых, одна из которых пересечена третьей прямой; свойства правильной 4-хугольной пирамиды
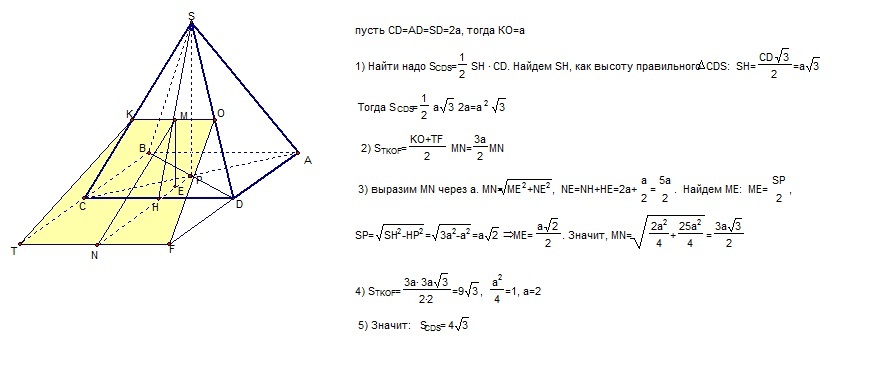
Приложения:
Похожие вопросы
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад