Сторона ромба равна 32. а острый угол равен 60гр. высота ромба,опущенная из вершины тупого угла делит сторону на 2 отрезка. каковы длины этих отрезков?
Ответы
Ответ дал:
0
Дано:
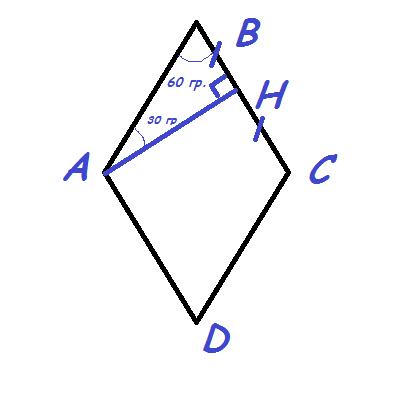
ABCD-ромб.
AB=32
уг. B=60 гр.
AH-высота, опущенная на сторону BC
Найти:
BH=?
HC=?
----------------------------------------
Решение:
1)Рассмотрим треуг. ABH-прямоугольный( AH- выстота)
угол А в треуг. ABH= 90 гр.-уг. B=90-60=30гр.
2)Катет, лежащий против угла в 30 гр., равен половине гипотенузы, следовательно BH=32/2=16.
3)По свойству ромба AB=BC=CD=AD=32, тогда НС= BC-BH=32-16=16
Получается, что эти отрезки равны.
Ответ: BH=HC=16.
Приложения:
Похожие вопросы
2 года назад
10 лет назад
10 лет назад