В треугольник ABC со сторонами AB=5см, BC=8см, AC=9см вписана окружность касающаяся стороны AC в точке K. Найдите расстояние от точки K до точки M биссектрисы BM.

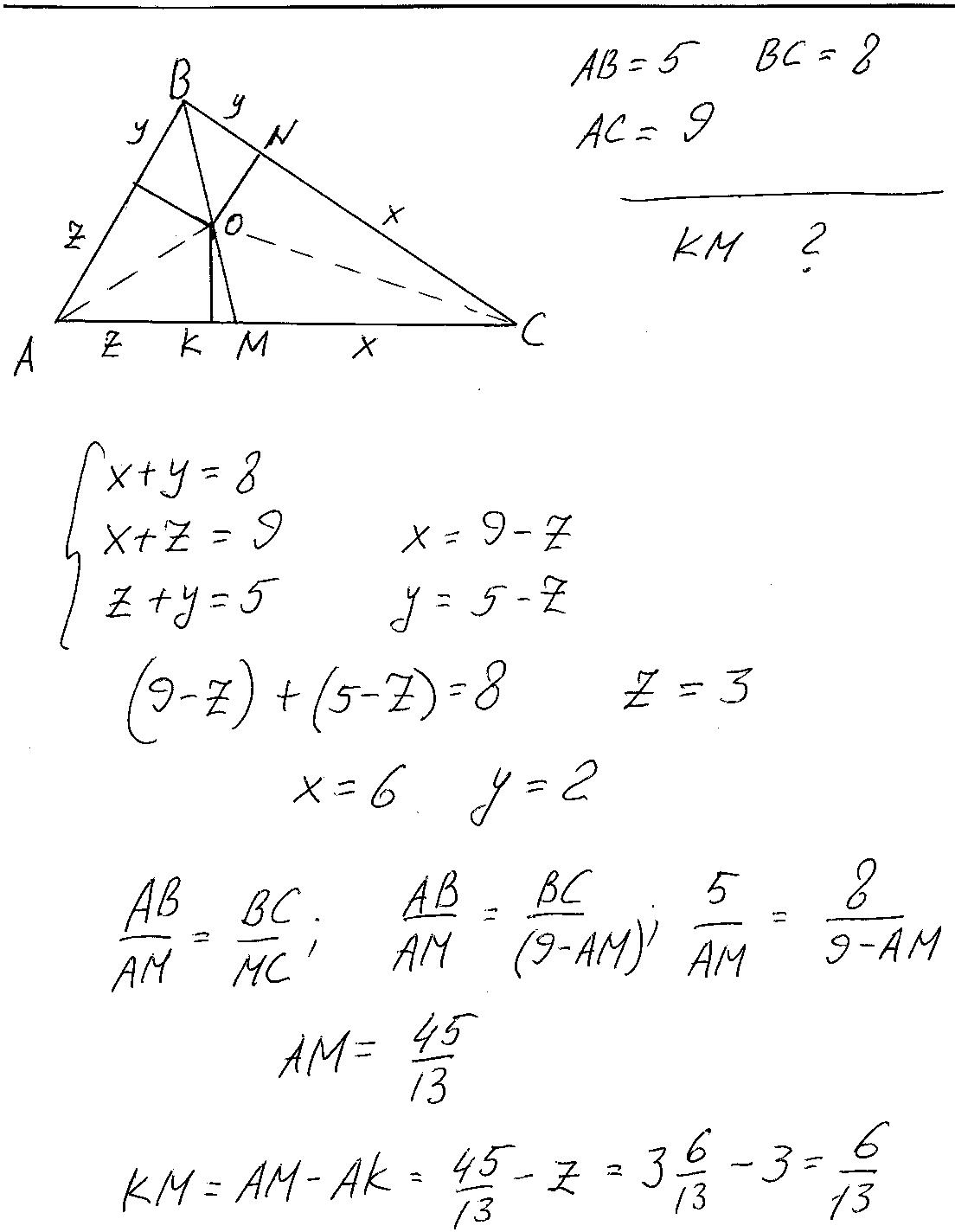
Центр вписанной окружности О лежит на биссектрисе ВМ(смотри рисунок). Проводим радиусы. Прямоугольные треугольники КОС и NОС равны (у них ОК=ОN как радиусы и гипотенуза ОС общая). Аналогично доказываем равенство остальных треугольников и обозначаем равные стороны Х, У,Z.  Далее по свойству биссектрисы находим АМ. Окончательный ответ КМ=6/13.