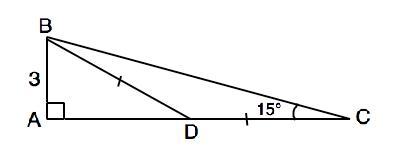
В прямоугольном треугольнике АВС катет АВ равен 3 см, угол С равен 15°. На катете АС отмечена точка D так,что угол СВD равен 15°.
А) найдите длину отреза ВD
В) докажите, что ВС < 12 см

 По условию АВ и АС  - катеты. ⇒ ∠А=90°. Т.к. ∠СВD=∠ВСD=15°, треугольник BDC равнобедренный. DB=DC

    Внешний угол ВDA треугольника BDC  равен сумме углов, не смежных с ним. В ∆ АВD угол ВDА=15°+15°=30°, гипотенуза ВD вдвое больше катета, противолежащего углу 30°(свойство) ВD=2 АВ=6 см .

 СD=DB, ⇒ их сумма 12 см. Длина любой стороны треугольника всегда меньше суммы длин двух его других сторон (неравенство треугольника). ⇒ ВС < 12 см