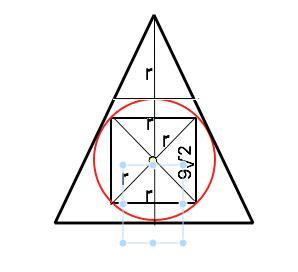
У коло вписано квадрат зі стороною 9 корнів із 2 см. Знайдіть сторону правильного трикутника, описаного навколо цього кола.

 В окружность вписан квадрат со стороной 9 корней из 2 см. Найдите сторону правильного треугольника, описанного около этой окружности.

Ответ:18√3 (см)

Объяснение:

 Диаметром окружности, описанной около квадрата, является его диагональ. Точкой пересечения диагоналей квадрат делится на 4 равнобедренных прямоугольных треугольника, гипотенузы которых - стороны квадрата, а острые углы 45°. => r=9√2•sin45°=9

Центры окружностей, вписанных и описанных около правильного треугольника, совпадают ( это точка пересечения биссектрис, которые в то же время являются его срединными перпендикулярами).  

  Радиус вписанной в правильный треугольник окружности находят по формуле r=a:2√3 , где а - сторона правильного треугольника. =>

a=r•2√3  

a=9•2√3=18√3 (см)