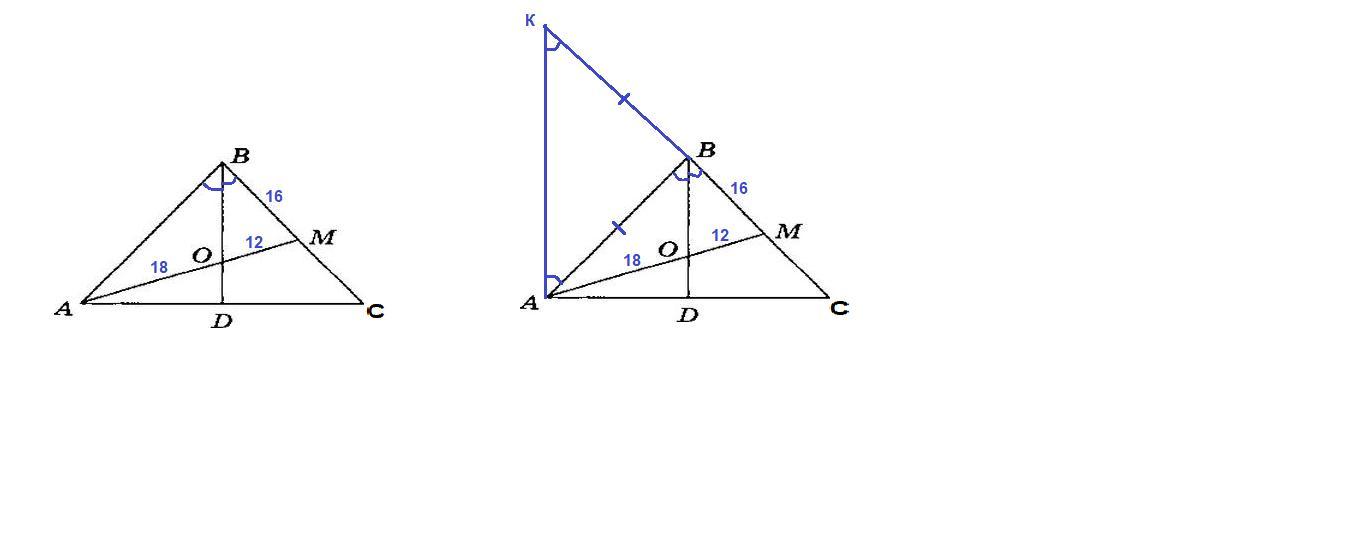
НАПИШИТЕ ПОЖАЛУЙСТА!!! треугольник ABC-равнобедренный с основанием АС, BD - его высота. Найдите боковую сторону треугольника, если АО=18 см,  а ОМ=12 см, ВМ=16 см.

BD - высота равнобедренного треугольника, проведенная к основанию, значит и биссектриса.

Биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.

В треугольнике АВМ ВО - биссектриса, значит

АО : ОМ = ВА : ВМ

ВА = АО · ВМ / ОМ = 18 · 16 / 12 = 24 см

Доказательство свойства биссектрисы (на всякий случай)

Проведем прямую АК║BD, К - точка пересечения этой прямой с прямой ВС.

∠DBA = ∠KAB как накрест лежащие (AK ║ BD, AB секущая),

∠CBD = ∠СКА как соответственные (АК ║ BD, СК секущая),

так как ∠DBA = ∠CBD, то и ∠КАВ = ∠СКА, тогда

ΔАВК равнобедренный, АВ = ВК.

По обобщенной теореме Фалеса:

АО : ОМ = КВ : ВМ или

АО : ОМ = АВ : ВМ.