В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке Р .докажите что площади треугольников АРВ и CPD равны

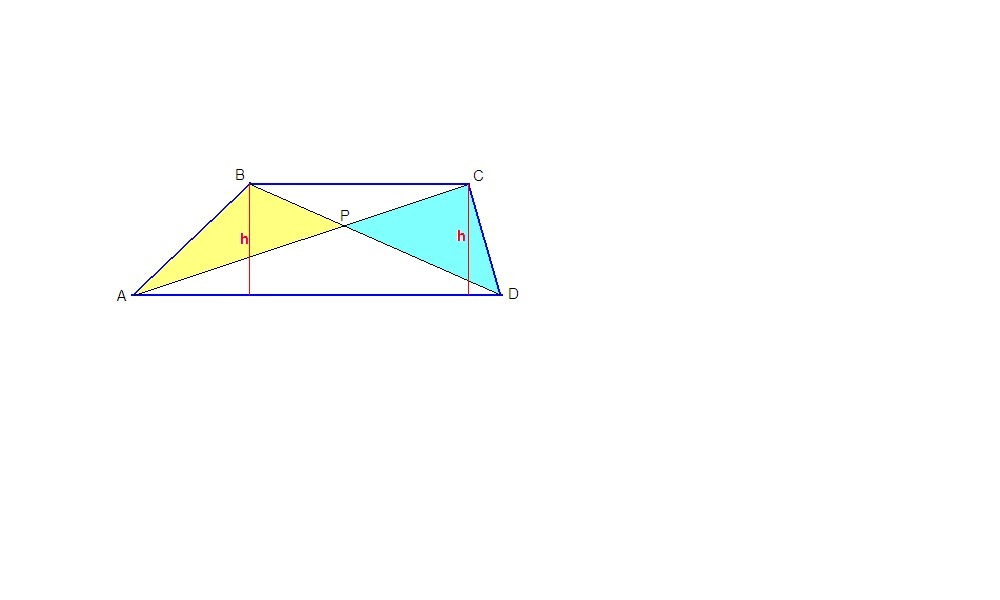
Высоты трапеции, проведенные из вершин В и С равны (расстояния между параллельными прямыми). Обозначим их h.
Sabd = AD·h = Sapd  + Sapb
Sacd = AD·h = Sapd  + Scpd
Площади треугольников ABD и ACD равны, значит равны и площади треугольников APB и CPD.